Beyond Trial and Error: A Practical Guide to DoE vs OFAT for Optimizing Organic Synthesis

Emma Hayes Dec 03, 2025 396

This article provides a comprehensive comparison between the traditional One-Factor-at-a-Time (OFAT) approach and the systematic Design of Experiments (DoE) methodology in organic synthesis and drug development.

Beyond Trial and Error: A Practical Guide to DoE vs OFAT for Optimizing Organic Synthesis

Abstract

This article provides a comprehensive comparison between the traditional One-Factor-at-a-Time (OFAT) approach and the systematic Design of Experiments (DoE) methodology in organic synthesis and drug development. Tailored for researchers and development professionals, it explores the foundational principles of both methods, outlines practical steps for implementing DoE, and addresses common troubleshooting scenarios. Through a validation and comparative lens, it demonstrates how DoE can lead to more efficient, robust, and insightful optimization of reaction conditions, ultimately saving time and resources while uncovering critical interaction effects that OFAT misses. The discussion is extended to include the emerging role of machine learning in augmenting DoE strategies.

OFAT vs DoE: Understanding the Core Principles and Historical Context

In the rigorous world of organic synthesis research, where the optimization of reaction conditions is paramount to achieving high yields and purity, the One-Factor-at-a-Time (OFAT) approach has long served as a foundational experimental methodology. Also known as one-variable-at-a-time (OVAT) or monothetic analysis, OFAT represents the classical strategy for investigating the effects of process variables on a desired outcome [1]. This method involves systematically testing individual factors—such as temperature, catalyst loading, or solvent choice—while maintaining all other parameters at constant levels [2]. Despite the emergence of more sophisticated statistical approaches like Design of Experiments (DOE), OFAT continues to hold intuitive appeal for many researchers, particularly in early-stage investigations where factor relationships are not well characterized [3].

Within the broader context of DOE versus OFAT methodologies in organic synthesis, understanding the precise definition, mechanics, and appropriate applications of OFAT is crucial for research scientists and drug development professionals. This technical guide provides a comprehensive examination of the OFAT approach, detailing its procedural framework, intuitive advantages, and significant limitations when applied to complex, multi-factorial chemical systems where factor interactions often dictate experimental outcomes [4].

Historical Context and Definition

The OFAT method has a long history of application across diverse scientific fields including chemistry, biology, engineering, and manufacturing [2]. As one of the earliest formalized experimental strategies, it gained widespread adoption due to its conceptual simplicity and straightforward implementation, allowing researchers to isolate the effect of individual variables without requiring complex experimental designs or advanced statistical analysis techniques [2].

OFAT is fundamentally defined as a method of designing experiments involving the testing of factors, or causes, one at a time instead of multiple factors simultaneously [1]. The core principle rests on the ceteris paribus condition—"all other things being equal"—whereby a single factor is varied across a range of values while rigorously maintaining all other parameters at fixed, constant levels [5]. This systematic isolation enables the experimenter to attribute any observed changes in the response variable directly to the manipulated factor, creating a clear, causal narrative that aligns closely with conventional scientific reasoning.

The OFAT Methodological Framework

Core Procedural Steps

The execution of a standard OFAT investigation follows a sequential, linear pathway as illustrated in Figure 1 and detailed in the procedural steps below.

G Figure 1: OFAT Experimental Workflow Start Define Response Variable and Potential Factors Base Establish Baseline Conditions (Fixed Levels for All Factors) Start->Base Select Select Single Factor to Investigate Base->Select Vary Vary Selected Factor Across Defined Levels Select->Vary Measure Measure Response at Each Factor Level Vary->Measure Reset Reset Factor to Baseline Level Measure->Reset Check All Factors Tested? Reset->Check Check->Select No Analyze Analyze Individual Factor Effects Check->Analyze Yes End Identify Optimal Conditions Analyze->End

  • Define the Response Variable and Potential Factors: Clearly identify the primary outcome to be optimized (e.g., reaction yield, purity, reaction time) and select the input factors hypothesized to influence this outcome [3].
  • Establish Baseline Conditions: Fix all factors at predetermined constant levels that typically represent current standard operating conditions or literature values [2].
  • Select a Single Factor to Investigate: Choose one variable to methodically vary while holding others constant [5].
  • Vary the Selected Factor Across Defined Levels: Systematically adjust the chosen factor through a series of predetermined values (e.g., temperature: 30°C, 50°C, 70°C) [2].
  • Measure the Response at Each Factor Level: Execute experiments and record the output response for each variation of the factor [2].
  • Reset the Factor to Baseline Level: Return the manipulated factor to its original value before proceeding to investigate the next factor [2].
  • Repeat Process Sequentially: Iterate steps 3-6 for each additional factor included in the investigation [2].
  • Analyze Individual Factor Effects: Compile results to determine the apparent optimal level for each factor based on its individual performance [5].
  • Identify Optimal Conditions: Combine the seemingly optimal levels for each factor to propose a global optimum for the system [5].

Representative Experimental Protocol

The following detailed protocol exemplifies a typical OFAT application in optimizing a hypothetical Suzuki-Miyaura cross-coupling reaction, a transformation highly relevant to pharmaceutical development [4].

Objective: Maximize reaction yield (%) of a Suzuki-Miyaura cross-coupling reaction between bromobenzene and 4-fluorophenylboronic acid.

Fixed Baseline Conditions:

  • Bromobenzene: 2 mmol
  • 4-fluorophenylboronic acid: 2.4 mmol
  • Solvent: DMSO (5 mL)
  • Catalyst: Kâ‚‚PdClâ‚„ (1 mol%)
  • Ligand: PPh₃ (0.2 mmol)
  • Base: NaOH (4 mmol)
  • Temperature: 60°C
  • Reaction time: 24 hours

OFAT Experimental Sequence:

  • Temperature Optimization (Baseline: 60°C)

    • Conduct reactions at: 40°C, 50°C, 60°C, 70°C, 80°C
    • Maintain all other factors at baseline conditions
    • Analyze yields: Identify apparent optimal temperature (e.g., 70°C)
    • Reset temperature to 60°C before proceeding

  • Catalyst Loading Optimization (Baseline: 1 mol%)

    • Conduct reactions at: 0.5 mol%, 1 mol%, 2 mol%, 5 mol%
    • Maintain all other factors at baseline conditions (including temperature at 60°C)
    • Analyze yields: Identify apparent optimal catalyst loading (e.g., 2 mol%)
    • Reset catalyst loading to 1 mol% before proceeding

  • Solvent Optimization (Baseline: DMSO)

    • Conduct reactions with: DMSO, MeCN, DMF, Toluene
    • Maintain all other factors at baseline conditions
    • Analyze yields: Identify apparent optimal solvent (e.g., MeCN)
    • Reset solvent to DMSO before proceeding

  • Continue Sequentially through remaining factors (base, ligand, concentration, etc.)

Proposed Optimal Conditions: Combine individual optimal levels (70°C, 2 mol% catalyst, MeCN solvent, etc.) as the presumed global optimum.

The Intuitive Appeal of OFAT

Despite its statistical limitations, OFAT maintains several compelling advantages that explain its persistent adoption in research environments, particularly among non-specialists and during preliminary investigations.

Table: Advantages of the OFAT Approach

Advantage Description Research Context
Conceptual Simplicity Straightforward methodology that aligns with conventional scientific training [6] Accessible to researchers without advanced statistical background [1]
Minimal Planning Overhead Requires no complex experimental design or statistical software [3] Ideal for rapid preliminary investigation of new chemical spaces [3]
Clear Data Interpretation Direct cause-effect attribution for individual factors [5] Simplifies communication of results to interdisciplinary teams
Adaptive Experimentation Allows real-time modification of experimental plan based on emerging results [5] Researcher can adjust factor ranges or abandon unproductive directions
Low Infrastructure Requirement Implementable with standard laboratory equipment and practices [2] No specialized software, statistical expertise, or automation systems needed [3]

The intuitive logic of OFAT aligns closely with conventional scientific training, where variables are traditionally isolated to establish causal relationships [6]. This methodological familiarity lowers implementation barriers, especially in situations where data generation is inexpensive and abundant [1]. Furthermore, OFAT provides researchers with direct control over the experimental sequence, allowing for real-time adjustments based on observational insights—a flexibility that aligns with the iterative nature of exploratory chemistry [5].

Limitations in Complex Chemical Systems

While OFAT offers intuitive appeal and operational simplicity, its methodological constraints become particularly problematic when applied to complex, multi-factorial organic syntheses where factor interactions frequently determine system behavior.

Table: Key Limitations of OFAT in Organic Synthesis

Limitation Impact on Experimental Outcomes Statistical Principle Violated
Inability to Detect Interactions Misses synergistic/antagonistic effects between factors [2] [1] Factor non-additivity
Inefficient Resource Utilization Requires more experiments for equivalent precision [1] Experimental inefficiency
Risk of False Optima May identify suboptimal conditions due to unmeasured interactions [5] Response surface misunderstanding
Limited Experimental Space Coverage Explores only a small fraction of possible factor combinations [2] Incomplete factor space exploration
No Experimental Error Estimation Provides no inherent measure of variability or significance [2] Lack of replication principle

The failure to capture interaction effects represents the most significant limitation of OFAT in complex chemical systems. As demonstrated in a 2025 study published in Scientific Reports, catalytic systems "often involve multiple factors that interact synergistically or antagonistically" [4]. When OFAT ignores these interactions by varying factors individually, it risks developing "suboptimal systems" that fail to account for the true complexity of the reaction landscape [4].

This methodological shortcoming is quantitatively demonstrated in a comparative study between OFAT and minimum runs resolution-IV methods for enhancing polysaccharide production, where the statistical approach resulted in a 7.3-9.2% increase in yield compared to OFAT-optimized conditions [7]. Similarly, OFAT's requirement for "more runs for the same precision in effect estimation" makes it statistically inefficient compared to factorial designs [1].

Essential Research Reagent Solutions

The following table details key reagents and materials commonly investigated using OFAT approaches in optimization studies for cross-coupling reactions, along with their experimental functions [4].

Table: Key Research Reagents in Cross-Coupling Reaction Optimization

Reagent Category Specific Examples Experimental Function OFAT Investigation Focus
Phosphine Ligands PPh₃, P(4-F-C₆H₄)₃, P(4-OMe-C₆H₄)₃, P(t-Bu)₃ [4] Modifies catalyst activity and selectivity Electronic effects (vCO), steric bulk (Tolman's cone angle) [4]
Palladium Catalysts Kâ‚‚PdClâ‚„, Pd(OAc)â‚‚ [4] Facilitates cross-coupling through catalytic cycles Catalyst loading (mol%), precursor type [4]
Solvents DMSO, MeCN, DMF, Toluene [4] Medium for reaction, influences solubility and stability Polarity, donor/acceptor characteristics, dielectric constant [4]
Bases NaOH, Et₃N [4] Scavenges acid byproduct, activates boronic acid Base strength, stoichiometry, nucleophilicity [4]
Aryl Halides Bromobenzene, Iodobenzene [4] Electrophilic coupling partner Electronic effects, steric hindrance, leaving group ability
Nucleophiles Phenylacetylene, 4-fluorophenylboronic acid, butylacrylate [4] Nucleophilic coupling partner Steric and electronic properties, stoichiometry

Comparative Analysis: OFAT versus Statistical DoE

Understanding the fundamental differences between OFAT and Design of Experiments (DoE) approaches is essential for selecting an appropriate optimization strategy. The following table summarizes key distinctions based on methodological characteristics and output capabilities [2] [5].

Table: Direct Comparison of OFAT and DoE Methodologies

Characteristic OFAT Approach DoE Approach
Factor Manipulation One factor varied at a time [5] Multiple factors varied simultaneously [5]
Experimental Sequence Sequential, linear progression [5] Structured, parallel investigation [2]
Number of Experiments Determined by experimenter [5] Determined by statistical design [5]
Interaction Detection Cannot estimate interactions between factors [2] [1] Systematically estimates and quantifies interactions [2]
Precision of Estimation Lower precision for the same number of runs [1] Higher precision through orthogonal designs [1] [5]
Optimal Condition Identification High risk of false optima in complex systems [5] Higher probability of identifying true optimum [2]
Experimental Space Coverage Limited coverage along single-dimensional paths [2] Comprehensive coverage of multi-dimensional space [2]
Statistical Foundation Based on intuitive, direct comparison Founded on randomization, replication, and blocking principles [2]
Curvature Detection Cannot reliably detect curvature in response [5] Can detect and model curvature (e.g., via central composite designs) [2]
Data Analysis Framework Simple direct comparison Analysis of Variance (ANOVA), response surface methodology [2]

The comparative inefficiency of OFAT becomes mathematically evident as factor count increases. For example, investigating k factors at L levels each requires L×k experimental runs in OFAT, while a full factorial DoE would require L^k runs—initially seeming to favor OFAT. However, fractional factorial and other optimized designs can extract equivalent or superior information with run counts comparable to or even lower than OFAT while capturing interactions that OFAT necessarily misses [1].

The One-Factor-at-a-Time approach represents a historically significant and intuitively accessible methodology for experimental optimization in organic synthesis. Its systematic isolation of variables, conceptual clarity, and minimal statistical requirements continue to make it appropriate for preliminary investigations and systems where factor interactions are known to be negligible [1]. However, for the complex, multi-factorial reaction systems typical of modern drug development—where interaction effects significantly influence outcomes—OFAT's limitations in efficiency, interaction detection, and optimization reliability present substantial constraints [4].

Within the broader framework of DoE versus OFAT methodologies, informed researchers must recognize that while OFAT offers a comfortable starting point for exploration, statistical DoE approaches provide a more comprehensive, efficient, and statistically rigorous pathway for optimizing complex chemical systems, particularly when augmented with modern machine learning techniques that further reduce experimental burdens [8]. The appropriate selection between these methodologies ultimately depends on the system complexity, resource constraints, and optimization goals specific to each research endeavor.

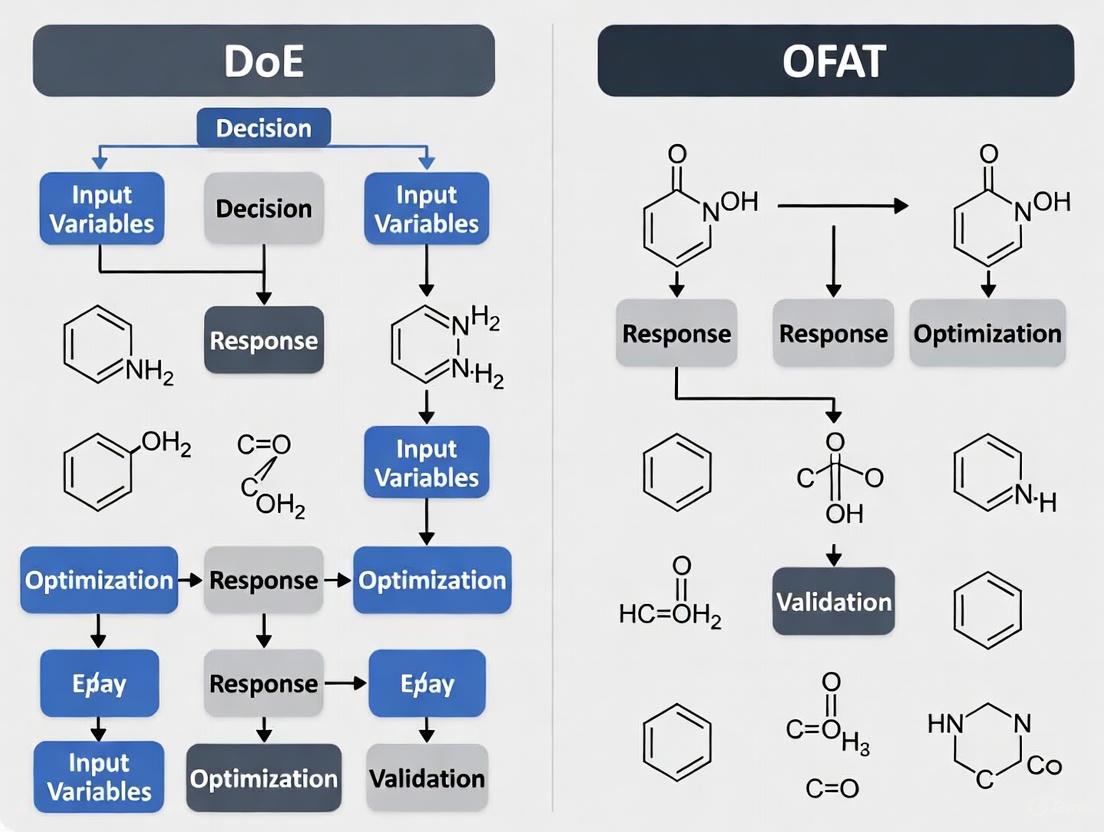
In the development of new synthetic methodology, chemists have traditionally relied on the One-Factor-At-a-Time (OFAT) approach for reaction optimization. This method involves varying a single parameter while keeping all others constant, proceeding through sequential iterations. While intuitively simple, this approach treats variables as independent entities, operating under the assumption that optimal conditions can be found through isolated parameter adjustments [9] [10].

However, this assumption proves problematic in complex chemical systems where factor interactions significantly influence outcomes. OFAT optimization often leads to erroneous conclusions about true optimal conditions because it fails to explore the multi-dimensional "reaction space" where combinations of parameter settings can produce synergistic effects unobservable through isolated variation [9]. As illustrated in Figure 1, OFAT may identify a local optimum while completely missing the global optimum that exists in a different region of the experimental landscape. This fundamental limitation results in suboptimal processes that consume excessive time and resources while delivering inferior results [10] [4].

Table 1: Comparison of OFAT and DoE Approaches to Reaction Optimization

Characteristic OFAT Approach DoE Approach
Exploration of Factor Interactions Cannot detect interactions Systematically identifies and quantifies interactions
Number of Experiments Increases linearly with factors Increases logarithmically with factors
Resource Efficiency Low (high material consumption) High (optimized information per experiment)
Statistical Reliability Limited, requires repetition Built-in reproducibility assessment
Optimum Identification Often finds local optimum Identifies global optimum
Multi-Response Optimization Sequential, often conflicting Simultaneous optimization possible

Fundamental Principles of Design of Experiments

What is Design of Experiments?

Design of Experiments (DoE) represents a paradigm shift in experimental approach, moving from sequential isolation to parallel investigation of multiple factors. DoE is a structured, efficient approach to experimentation that employs statistical techniques to investigate potentially significant factors and determine their cause-and-effect relationship on experimental outcomes [11]. When a relationship between experimental parameters (factors) and results exists, DoE can detect and quantify this correlation, enabling researchers to design optimal and robust processes [11].

The core principle of DoE involves identifying important factors and selecting at least two reasonable levels for each factor. After defining these factor levels, experiments are performed according to a specific experimental design. The significance of each factor is then assessed using statistical analysis of the experimental data, leading to objective, data-driven conclusions about process optimization [4].

The Statistical Foundation of DoE

The statistical framework of DoE models process responses through a mathematical equation that accounts for various types of effects. For a system with multiple input variables (x₁, x₂, x₃, etc.), the response (e.g., chemical yield) can be represented as:

Response = β₀ + β₁x₁ + β₂x₂ + β₃x₃ + ... + β₁₂x₁x₂ + β₁₃x₁x₃ + ... + β₁₁x₁² + β₂₂x₂² + ...

Where:

  • β₀ represents the base constant (overall mean response)
  • β₁x₁, β₂xâ‚‚, etc. are the main effects of each variable
  • β₁₂x₁xâ‚‚, β₁₃x₁x₃, etc. capture two-factor interaction effects
  • β₁₁x₁², β₂₂x₂², etc. account for quadratic (curvature) effects [10]

Different experimental designs incorporate different combinations of these terms. Fractional factorial designs typically capture only main effects, while full factorial designs add interaction terms. Response surface methodologies include squared terms to model curvature and identify true optimal conditions within the experimental domain [10].

DOE_Workflow Start Define Optimization Objectives F1 Identify Factors and Ranges Start->F1 F2 Select Experimental Design F1->F2 F3 Execute Randomized Experiments F2->F3 F4 Analyze Results Statistically F3->F4 F5 Build Predictive Model F4->F5 F6 Verify Model with Confirmatory Runs F5->F6 End Implement Optimal Conditions F6->End

Figure 1: The DoE Optimization Workflow - A systematic approach to process optimization

Key Experimental Designs and Their Applications

Screening Designs: Identifying Influential Factors

Screening designs help researchers identify which factors among many potential variables have significant effects on the response. These designs are particularly valuable in early stages of method development when numerous factors may be under consideration.

Plackett-Burman Design (PBD) is a widely used screening approach that allows investigation of up to n-1 factors in only n experiments, where n is a multiple of four [4]. For example, a 12-run Plackett-Burman design can efficiently screen 11 factors. In each experimental run, factors are set at two levels (low: -1 and high: +1), enabling researchers to quickly identify the most influential parameters for further optimization [4]. This efficiency makes PBD particularly valuable when working with expensive reagents or time-consuming analyses.

Definitive Screening Design (DSD) represents a more recent advancement that can screen multiple factors while retaining the ability to detect curvature and some two-factor interactions [12]. These designs are especially useful when the relationship between factors and responses may not be purely linear.

Response Surface Methodologies: Mapping the Optimization Landscape

Once significant factors have been identified through screening designs, response surface methodologies (RSM) provide powerful tools for locating optimal conditions and understanding the response landscape.

Central Composite Design (CCD) is the most popular RSM approach, comprising a factorial or fractional factorial design augmented with center points and axial points [12]. This arrangement allows estimation of all main effects, two-factor interactions, and quadratic terms, providing a complete picture of the response surface. CCDs can identify stationary points (maxima, minima, or saddle points) and characterize the nature of these regions [12].

Box-Behnken Design (BBD) offers an efficient alternative to CCD, requiring fewer experimental runs while still capturing quadratic effects. BBDs are rotatable designs that place experimental points on a sphere within the factor space, making them particularly useful when extreme factor combinations may be problematic or impossible to run [4].

Table 2: Common Experimental Designs and Their Applications in Synthetic Chemistry

Design Type Key Characteristics Typical Applications Advantages Limitations
Full Factorial Tests all possible combinations of factor levels Initial method scouting, 2-4 factor systems Captures all interactions, Comprehensive Number of runs grows exponentially (2ᵏ)
Fractional Factorial Tests fraction of full factorial combinations Screening many factors (5+), Initial phase optimization Highly efficient, Identifies key drivers Confounds interactions (aliasing)
Plackett-Burman Two-level screening design with n runs for n-1 factors Rapid screening of many factors, Identifying active factors Extreme efficiency, Minimal runs Only main effects, No interactions
Central Composite Three-level design with factorial, axial and center points Response surface mapping, Final optimization Captures curvature, Locates optimum Higher number of runs required
Box-Behnken Three-level spherical design without corner points Response surface mapping, When extremes are problematic Efficient for quadratic models, No extreme conditions Poor estimation of pure quadratic terms
Taguchi Arrays Orthogonal arrays with inner/outer design structure Robust parameter design, Noise factor incorporation Addresses variability, Process robustness Complex analysis, Controversial statistics

DoE in Practice: Implementation in Synthetic Chemistry

The DoE Workflow: A Step-by-Step Guide

Successful implementation of DoE follows a systematic workflow that maximizes information gain while minimizing experimental effort:

  • Define Clear Objectives: Determine which responses will be optimized (yield, selectivity, purity, etc.) and whether the goal is screening, optimization, or robustness testing [10].

  • Identify Factors and Ranges: Select process parameters to investigate and establish feasible ranges based on chemical knowledge and practical constraints [10].

  • Select Appropriate Design: Choose an experimental design aligned with objectives, considering the number of factors, resources, and desired information [10].

  • Execute Randomized Experiments: Perform experiments in randomized order to minimize confounding from uncontrolled variables [4].

  • Analyze Results Statistically: Use statistical software to identify significant factors, interactions, and build predictive models [10].

  • Verify and Validate: Confirm model predictions with additional experiments and validate optimal conditions [10].

Case Study: DoE in Cross-Coupling Reactions

A recent study demonstrated the power of Plackett-Burman design for screening key factors in palladium-catalyzed cross-coupling reactions, including Mizoroki-Heck, Suzuki-Miyaura, and Sonogashira-Hagihara transformations [4]. The investigation systematically evaluated five critical factors:

  • Electronic effect of phosphine ligands (measured by vCO stretching frequency)
  • Tolman's cone angle (steric bulkiness) of phosphine ligands
  • Catalyst loading (1-5 mol%)
  • Base strength (Et₃N vs. NaOH)
  • Solvent polarity (DMSO vs. MeCN)

The PBD design enabled researchers to efficiently rank factor importance across different reaction types, revealing which parameters most significantly influenced yield in each transformation. This systematic approach provided deeper insight into catalyst behavior while minimizing experimental effort [4].

Advanced Application: Integrating DoE with Machine Learning

Cutting-edge applications now combine DoE with machine learning (ML) to further enhance optimization capabilities. A recent study optimized a macrocyclization reaction for organic light-emitting devices (OLEDs) by correlating five reaction factors with device performance [13]. The integrated "DoE + ML" approach employed:

  • Taguchi's orthogonal arrays (L18 design) to efficiently explore the 5-factor, 3-level experimental space
  • Support vector regression (SVR) to build predictive models of device performance
  • Leave-one-out cross-validation to assess model accuracy and select the best predictor
  • Grid search of the predictive model to identify optimal reaction conditions [13]

This integrated methodology successfully identified reaction conditions that produced crude materials yielding OLED devices with 9.6% external quantum efficiency - outperforming devices fabricated using purified materials [13].

DEML_Integration DOE DoE: Strategic Experimental Design Data High-Quality Dataset DOE->Data ML Machine Learning Modeling Data->ML Model Predictive Model ML->Model Optimum Identified Optimum Model->Optimum Validation Experimental Validation Optimum->Validation Validation->DOE Iterative Refinement

Figure 2: Integrated DoE-ML Workflow - Combining strategic experimentation with predictive modeling

Essential Research Reagent Solutions for DoE Implementation

Successful DoE implementation requires careful selection of reagents and materials that enable efficient exploration of experimental space. The following table summarizes key reagent categories and their strategic roles in DoE studies.

Table 3: Research Reagent Solutions for DoE Implementation in Organic Synthesis

Reagent Category Specific Examples Function in DoE Studies Experimental Considerations
Catalyst Systems Kâ‚‚PdClâ‚„, Pd(OAc)â‚‚, Ni(cod)â‚‚ Vary metal source and loading to optimize catalytic activity Loading levels (e.g., 1-5 mol%), Precursor solubility, Compatibility with ligands [4] [13]
Ligand Architectures Phosphines (PPh₃, XPhos), N-Heterocyclic carbenes Modulate steric and electronic properties to tune selectivity Electronic effect (vCO), Tolman cone angle, Ligand:metal ratio [4]
Solvent Systems DMSO, MeCN, DMF, Water, green solvents Explore solvent space based on polarity, H-bonding, sustainability Use solvent maps (PCA), Consider solvent properties, Environmental impact [9]
Base Additives Et₃N, NaOH, K₂CO₃, Cs₂CO₃ Screen base strength and solubility for deprotonation steps Nucleophilicity vs. basicity, Solubility in reaction medium, Byproduct formation [4]
Substrate Variations Aryl halides with different electronic/steric properties Test substrate scope under optimized conditions Electronic effects, Steric hindrance, Functional group tolerance [9]

Design of Experiments represents a fundamental shift from traditional, empirical approaches to a systematic, statistical framework for process optimization. By simultaneously investigating multiple factors and their interactions, DoE enables researchers to uncover complex relationships that remain invisible to OFAT approaches. The methodology delivers not only optimized conditions but also deeper process understanding, revealing how factors interact to influence key responses.

The integration of DoE with emerging technologies like machine learning and high-throughput experimentation further enhances its power, creating synergistic methodologies that accelerate research while conserving precious resources [14] [13]. As the chemical industry faces increasing pressure to develop sustainable, efficient processes, adopting DoE as a standard practice provides researchers with a powerful framework for navigating complex experimental landscapes and delivering robust, optimized synthetic methodologies.

For synthetic chemists accustomed to traditional approaches, the initial investment in learning DoE principles yields substantial returns in experimental efficiency, process understanding, and ultimately, the development of superior chemical processes with reduced time and resource investment.

In the realm of organic synthesis research, the pursuit of optimal reaction conditions presents a significant challenge. Traditional One-Factor-at-a-Time (OFAT) approaches, where only one variable is altered while all others remain constant, have historically dominated experimental practice [15]. While intuitively straightforward, OFAT methodologies possess inherent limitations, most notably their inability to detect interactions between factors—the scenario where the effect of one factor depends on the level of another [16] [2]. In complex chemical systems, where such interactions are prevalent, OFAT can lead to suboptimal conclusions and inefficient use of resources [4].

Design of Experiments (DOE) provides a superior, systematic framework grounded in statistical principles [17]. It enables researchers to simultaneously investigate the impact of multiple input factors on a desired output response, thereby capturing the true, interconnected nature of chemical processes [15] [16]. This whitepaper delineates the core terminology of DOE, framing it within the critical comparison with OFAT and illustrating its application through contemporary examples in organic synthesis and drug development. Adopting DOE empowers scientists to build robust, predictive models for their reactions, ultimately accelerating the development of synthetic routes and pharmaceutical processes [13] [18].

Core Terminology of Design of Experiments (DOE)

Foundational Concepts

  • Design of Experiments (DOE): A branch of applied statistics concerning the planning, conduction, analysis, and interpretation of controlled tests to evaluate the factors that control the value of a parameter or group of parameters [17]. It is a systematic method that allows for multiple input factors to be manipulated simultaneously, determining their effect on a desired output [17].

  • Factor: A process input an investigator manipulates to cause a change in the output [19]. Also defined as an independent variable that can be set to a specific level [17]. In chemical synthesis, common factors include temperature, pressure, catalyst loading, solvent polarity, and reaction time [4].

  • Level: The specific value or setting that a factor is set to for an experimental run [17]. For example, a temperature factor might have levels of 50°C (-1) and 100°C (+1) in a screening design [17].

  • Response: The output(s) of a process or the outcome being measured and analyzed in an experiment [19]. In organic synthesis, this is typically yield, purity, selectivity, or a performance metric like device efficiency [13].

  • Effect: A measure of how changing the settings of a factor changes the response [19]. For a factor with two levels, the effect is calculated as the difference between the average response at the high level and the average response at the low level [17].

  • Treatment Combination: The specific combination of the levels of several factors in a given experimental trial, also known as a "run" [19].

Advanced Terminology

  • Interaction: Occurs when the effect of one factor on a response depends on the level of another factor(s) [19]. Interactions are ubiquitous in complex bioprocessing and chemical systems but are impossible to detect using OFAT approaches [15] [16].

  • Randomization: A principle where the experimental runs are performed in a random sequence to minimize the impact of lurking variables and systematic biases, thereby enhancing the validity of the statistical analysis [17] [2].

  • Replication: The repetition of a complete experimental treatment, including the setup [17]. Replication allows for the estimation of experimental error and improves the precision of the estimated effects [2] [19].

  • Blocking: A schedule for conducting treatment combinations such that effects due to a known change (e.g., different raw material batches, operators) become concentrated in the levels of the blocking variable. Blocking is achieved by restricting randomization to isolate a systematic effect and prevent it from obscuring the main effects [17] [19].

  • Aliasing (or Confounding): When the estimate of an effect also includes the influence of one or more other effects (usually high-order interactions) [19]. This occurs in fractional factorial designs where not all combinations are tested, but can be designed to be unproblematic if the higher-order interaction is non-existent or insignificant [19].

  • Center Points: Experimental points at the center value of all factor ranges, often added to a design to check for curvature in the response [16] [19].

OFAT vs. DOE: A Conceptual and Practical Comparison

The OFAT Methodology and Its Limitations

The One-Factor-at-a-Time (OFAT) approach involves varying a single factor while keeping all other factors constant, observing the response, and then repeating this process for each subsequent factor [2] [20]. Its perceived advantages are simplicity and ease of implementation, requiring no specialized statistical training [18] [20].

However, OFAT has severe limitations in complex systems like organic synthesis, including:

  • Inability to Detect Interactions: This is the most critical flaw. OFAT assumes factors are independent, but in chemistry, factors like temperature and catalyst often interact. An OFAT experiment cannot reveal if a catalyst performs better at a specific temperature [15] [16].
  • Inefficient Resource Use: OFAT requires a large number of experiments to explore the same space, especially as factors increase, making it time-consuming and costly [2] [4].
  • Risk of Misleading Optima: By missing interactions, OFAT can easily identify a suboptimal set of conditions, as demonstrated in a case where OFAT found a maximum yield of 86% while DOE, capturing the interaction, found a true maximum of 92% [16].
  • Limited Scope: OFAT only investigates a single path through the experimental region and may completely miss the global optimum [2].

The DOE Approach and Its Strategic Advantages

Design of Experiments (DOE) systematically varies multiple factors simultaneously according to a pre-determined mathematical plan [17]. This approach offers several strategic advantages, which are summarized in the table below and contrasted with OFAT.

Table 1: A systematic comparison of OFAT and DOE methodologies.

Aspect OFAT (One-Factor-at-a-Time) DOE (Design of Experiments)
Basic Principle Varies one factor at a time while holding others constant [2]. Systematically varies multiple factors simultaneously according to a statistical plan [17].
Detection of Interactions Cannot detect interactions between factors [16] [2]. Explicitly models and quantifies interaction effects between factors [15] [19].
Experimental Efficiency Low; requires many runs for multiple factors, leading to inefficient use of resources [4]. High; extracts maximum information from a minimal number of runs, saving time and materials [15] [18].
Statistical Validity Low; no inherent estimation of experimental error or statistical significance [2]. High; incorporates principles of randomization, replication, and blocking for reliable, defensible results [17] [2].
Primary Goal Understand the individual effect of each factor in isolation. Model the entire system, including main effects and interactions, for optimization and prediction [16].
Optimal Scope Simple systems with few, likely independent, factors [20]. Complex systems with multiple, potentially interacting factors [15] [13].

The following diagram illustrates the fundamental difference in how OFAT and DOE explore an experimental space with two factors, Temperature and pH.

cluster_OFAT OFAT Approach (Sequential Exploration) cluster_DOE DOE Approach (Simultaneous Exploration) OFAT_Start Start: (25°C, 5.5 pH) OFAT_Temp_Step1 Vary Temp Only (30°C, 5.5 pH) OFAT_Start->OFAT_Temp_Step1 OFAT_Temp_Step2 Vary Temp Only (35°C, 5.5 pH) OFAT_Temp_Step1->OFAT_Temp_Step2 OFAT_pH_Step1 Vary pH Only (30°C, 6.0 pH) OFAT_Temp_Step2->OFAT_pH_Step1 OFAT_pH_Step2 Vary pH Only (30°C, 6.5 pH) OFAT_pH_Step1->OFAT_pH_Step2 DOE_Run1 Run 1: (Low Temp, Low pH) DOE_Run2 Run 2: (Low Temp, High pH) DOE_Run3 Run 3: (High Temp, Low pH) DOE_Run4 Run 4: (High Temp, High pH)

Experimental Protocols and Applications in Synthesis

Case Study 1: Optimizing a Macrocyclization Reaction for OLED Performance

A 2025 study by Ikemoto et al. provides a sophisticated example of using DOE coupled with machine learning (ML) to optimize a macrocyclization reaction, where the response was not just chemical yield but the final performance of an organic light-emitting device (OLED) [13].

  • Objective: To correlate reaction conditions in the flask directly with OLED device performance (External Quantum Efficiency, EQE), thereby eliminating energy-consuming purification steps [13].
  • Factors and Levels: Five factors were investigated, each at three levels [13]:
    • Equivalent of Ni(cod)â‚‚ (M)
    • Dropwise addition time of monomer (T)
    • Final concentration of monomer (C)
    • % content of bromochlorotoluene in monomer (R)
    • % content of DMF in solvent (S)
  • Experimental Design: An L18 Taguchi orthogonal array was used, requiring only 18 experimental runs to efficiently explore the five-factor, three-level space [13].
  • Response: The External Quantum Efficiency (EQE) of the fabricated OLED was measured in quadruplicate for each of the 18 reaction conditions [13].
  • Analysis and Optimization: Machine learning models (Support Vector Regression was selected as best) were trained on the data to build a predictive map of EQE across the entire five-dimensional parameter space. The model successfully predicted an optimal condition that achieved a high EQE of 9.6%, surpassing the performance of devices made with purified materials [13].

Table 2: Key research reagents and materials for the OLED macrocyclization case study [13].

Reagent/Material Function in the Experiment
Dihalotoluene Monomer (1) The starting material for the Yamamoto-type macrocyclization reaction.
Ni(cod)â‚‚ Catalyst The transition metal catalyst that mediates the C-C coupling to form the macrocyclic products.
Phosphine Ligands Likely used as stabilizing ligands for the nickel catalyst (inferred from analogous procedures).
DMF (Solvent) A polar aprotic solvent; its ratio was a key factor in the DoE.
Ir Emitter (3) The dopant in the emission layer of the OLED device.
TPBi (2) An electron transport material, sublimated to form the electron transport layer.

Case Study 2: Screening Factors in Cross-Coupling Reactions

A 2025 proof-of-concept study in Scientific Reports applied a Plackett-Burman Design (PBD) to screen key factors in three fundamental cross-coupling reactions: Mizoroki-Heck, Suzuki-Miyaura, and Sonogashira-Hagihara [4].

  • Objective: To efficiently screen and rank the influence of multiple factors on reaction success, overcoming the limitations of OFAT in complex catalytic systems [4].
  • Factors and Levels: Five real factors were screened at two levels (high +1, low -1) using a 12-run PBD, which also included dummy factors to estimate experimental error [4]:
    • Ligand Electronic Effect (vCO)
    • Ligand Tolman's Cone Angle
    • Catalyst Loading (1 mol% vs. 5 mol%)
    • Base (Triethylamine vs. Sodium Hydroxide)
    • Solvent Polarity (DMSO vs. MeCN)
  • Experimental Design: A 12-run Plackett-Burman design, which is a highly efficient screening design used to identify the most influential factors from a large pool with minimal experiments [4].
  • Response: The conversion or yield of the respective cross-coupled product.
  • Analysis and Outcome: Statistical analysis of the results identified the most influential factors for each type of coupling reaction. This provides a data-driven basis for focusing subsequent, more detailed optimization studies (e.g., using Response Surface Methodology) on the few critical factors [4].

The workflow for a typical DoE-driven project in synthesis is summarized below.

Define_Goal 1. Define Goal and Response Identify_Factors 2. Identify Potential Factors and Levels Define_Goal->Identify_Factors Select_Design 3. Select Appropriate Experimental Design Identify_Factors->Select_Design Execute_Runs 4. Execute Runs (Randomized) Select_Design->Execute_Runs Analyze_Data 5. Analyze Data and Build Model Execute_Runs->Analyze_Data Build_Model 6. Identify Optimal Conditions and Interactions Analyze_Data->Build_Model Validate_Optimum 7. Validate Model with Confirmatory Run Build_Model->Validate_Optimum

The transition from OFAT to DOE represents a paradigm shift from a linear, isolated view of experimentation to a holistic, systems-level approach. For researchers in organic synthesis and drug development, mastering the core terminology of factors, levels, responses, and effects is the first step toward unlocking the full power of DOE [19].

As demonstrated by contemporary research, DOE is not merely a statistical tool but a critical strategic asset [13] [4]. It enables the efficient exploration of complex chemical spaces, reveals crucial interactions that OFAT blindly misses, and builds predictive models that lead to truly optimal outcomes—higher yields, superior product performance, and more sustainable processes with reduced waste and resource consumption [13] [18]. In an era of increasing process complexity and pressure for innovation, the adoption of DOE is no longer optional but essential for cutting-edge research and development.

Historical Use and Inherent Limitations of the OFAT Methodology

Within organic synthesis research, reaction optimization is a fundamental activity aimed at identifying experimental conditions that maximize yield, purity, or other critical response variables. The choice of optimization strategy profoundly impacts the efficiency, cost, and ultimate success of research and development, particularly in fields such as pharmaceutical development. The One-Factor-at-a-Time (OFAT) methodology represents a traditional approach to this challenge, characterized by its sequential modification of experimental variables [21]. This article situates the historical use and inherent limitations of OFAT within the broader thesis of its comparison to modern Design of Experiments (DoE) methodologies, providing researchers with a critical technical appraisal of its role in contemporary scientific practice.

Historical Use of OFAT in Experimental Science

The OFAT Methodology and Its Traditional Application

The OFAT approach is defined as an experimental procedure wherein a scientist iteratively performs experiments by fixing all process factors except one [21]. After identifying the best value for that single factor, that value is fixed while a subsequent set of experiments is executed to optimize another factor. This cycle continues until each factor has been optimized individually, at which point the scientist arrives at a presumed optimum set of reaction conditions [21]. This methodology has a long history of application across chemistry, biology, engineering, and manufacturing [2].

Its historical popularity stemmed from its straightforward implementation, as it could be conducted without complex mathematical modeling and aligned intuitively with how many scientists learned to conduct experiments during their training [21] [2]. In many cases, it served as a default technique, particularly in academic research settings where exposure to more advanced statistical optimization techniques was limited [21].

Table: Characteristic Steps in a Traditional OFAT Optimization Campaign

Step Action Objective
1 Select baseline operating conditions for all factors. Establish a starting point for optimization.
2 Vary one factor across a range of values while holding all others constant. Identify the value of that single factor that gives the best response.
3 Fix the optimized factor at its new "best" value. Lock in the gain for that variable.
4 Repeat steps 2 and 3 for each subsequent factor. Sequentially optimize all variables of interest.
5 Implement the final combination of individually optimized factors. Presume this represents the global optimum for the system.
Representative Case Study: OFAT in Organic Synthesis

A representative example of OFAT application in organic synthesis can be found in the work of Abtahi and Tavakol (cited in [21]) for the synthesis of bioactive propargylamine scaffolds. Their optimization procedure followed a classic OFAT pattern:

  • The temperature and reaction time were initially fixed while the reaction media and catalyst were optimized to obtain the highest yield.
  • The optimized media and catalyst were then fixed, and the temperature and reaction time were optimized.
  • Finally, with all other factors fixed, the catalyst loading was optimized. This procedure achieved a 75% yield in the model reaction, and the identified conditions were subsequently applied to several substrates, yielding 38–91% [21]. This case illustrates the stepwise, sequential nature of the OFAT approach and its capability to deliver functional, albeit potentially suboptimal, results.

Inherent Limitations of the OFAT Approach

Despite its historical prevalence and intuitive appeal, the OFAT methodology possesses several critical limitations that render it inefficient and potentially misleading for optimizing complex systems, especially in organic synthesis where factor interactions are common.

Failure to Capture Interaction Effects

The most significant drawback of the OFAT approach is its fundamental assumption that factors are independent. The method fails to capture interaction effects between variables [21] [22] [2]. In reality, chemical reaction outputs are exclusively nonlinear responses where factors often exhibit synergistic or antagonistic effects [21]. For instance, the ideal temperature for a reaction may depend on the catalyst loading, but OFAT cannot detect this relationship because when temperature is varied, the catalyst loading is held constant. By ignoring these interactions, OFAT frequently misidentifies the true optimal reaction conditions and can lead to a suboptimal understanding of the chemical process itself [21] [23].

Gross Inefficiency and Resource Intensiveness

OFAT is a highly inefficient experimental strategy. Varying each factor individually while holding others constant requires a substantially larger number of experimental runs to explore the parameter space compared to multivariate approaches like DoE [22] [2]. This leads to greater consumption of time, materials, and financial resources. Furthermore, with the increased number of experimental runs comes an elevated risk of experimental error or uncontrolled variability, which can compromise the reliability and reproducibility of the results [2].

Inability to Systematically Explore the Design Space

The OFAT approach is inherently limited in its ability to explore the entire experimental region or factor space. It only investigates factor levels along a single, narrow path and does not provide a comprehensive map of the response surface [2]. Consequently, there is a high probability that OFAT will converge on a local optimum rather than the global optimum, as it cannot "see" beyond the immediate path it is following [23]. This is particularly problematic in complex chemical systems with multiple peaks and valleys in the response landscape.

Table: Quantitative Comparison of OFAT and DoE for a Three-Factor, Two-Level Experiment

Aspect OFAT Approach Full Factorial DoE (2³)
Total Experimental Runs 10 (e.g., 4+3+3) 8
Information Gained Main effects only; no interaction effects. All main effects and all interaction effects.
Experimental Error Estimate Typically not available without replication. Can be obtained via center points.
Optimal Conditions Identified Likely suboptimal due to ignored interactions. Statistically validated global optimum.
Resource Efficiency Low High

The following diagram illustrates the sequential, narrow path of an OFAT optimization compared to the comprehensive exploration of a DoE factorial design, highlighting why OFAT can miss the true optimum.

cluster_ofat OFAT Path cluster_doe DoE Factorial Points O1 O2 O1->O2 O3 O2->O3 O4 O3->O4 D1 D2 D3 D4 TrueOptimum True Optimum

The Modern Alternative: Design of Experiments (DoE)

Fundamental Principles of DoE

Design of Experiments (DoE) is a systematic, multivariate approach to experimentation that addresses the core limitations of OFAT. Its power derives from several key statistical principles [2]:

  • Simultaneous Variation: Multiple factors are varied at once according to a structured experimental design (e.g., factorial designs), allowing for the efficient exploration of a large parameter space.
  • Interaction Effects: DoE models explicitly include and can quantify the interaction effects between factors, providing a more accurate representation of the system's behavior [21] [2].
  • Statistical Robustness: The methodology is built on foundational principles of randomization (to minimize bias), replication (to estimate experimental error), and blocking (to account for known sources of variability) [2].
Key Methodologies in DoE for Optimization

DoE encompasses a suite of methodologies tailored to different experimental goals, from initial screening to final optimization.

  • Factorial Designs: These are the cornerstone of DoE. Full or fractional factorial designs allow researchers to study the main effects of several factors and their interactions simultaneously. The data is typically analyzed using Analysis of Variance (ANOVA) to determine the statistical significance of each effect [2].
  • Response Surface Methodology (RSM): When the goal is to find optimal conditions, RSM is employed. This technique uses sequential experiments (e.g., the method of steepest ascent) to rapidly move from a starting point to the vicinity of the optimum [24] [25]. Once near the optimum, more elaborate designs like Central Composite Designs (CCD) or Box-Behnken Designs (BBD) are used to fit a second-order polynomial model. This model can precisely locate the optimum settings, whether for maximizing yield, minimizing impurities, or achieving a target specification [24] [26].

The workflow below contrasts the logical progression of a DoE-based optimization campaign with the OFAT approach, demonstrating its iterative and model-based nature.

cluster_doe DoE / RSM Workflow cluster_ofat OFAT Workflow Start Start: Define Objective and Factors Doe1 Screening Design (e.g., Fractional Factorial) Start->Doe1 OFAT1 Optimize Factor A Start->OFAT1 Doe2 Statistical Analysis (ANOVA, Effect Plots) Doe1->Doe2 Doe3 Path of Steepest Ascent/Descent Doe2->Doe3 Doe4 Optimization Design (e.g., CCD, BBD) Doe3->Doe4 Doe5 RSM Model & Validation Doe4->Doe5 Doe6 Confirmed Optimum Doe5->Doe6 OFAT2 Optimize Factor B OFAT1->OFAT2 OFAT3 Optimize Factor C OFAT2->OFAT3 OFAT4 Final Conditions (Potentially Suboptimal) OFAT3->OFAT4

Transitioning from OFAT to DoE requires familiarity with both conceptual tools and practical software resources.

Table: Essential Tools for Modern Experimental Optimization

Tool Category Example Function in Optimization
DoE Software JMP, MODDE, Design-Expert [21] Provides a user-friendly interface for generating optimal experimental designs and analyzing the resulting data statistically.
Statistical Programming Environments R, MATLAB, Python [21] Offer extensive libraries/packages for custom design generation and advanced statistical analysis, providing greater flexibility.
Automated Experimentation Platforms Automated synthesis reactors, high-throughput screening systems [21] Enable the rapid execution of the many experiments defined by a DoE protocol, drastically reducing time and labor.
Experimental Design Types Full/Fractional Factorial, Central Composite, Box-Behnken, Plackett-Burman [21] [24] [23] Blueprints for experimentation. Each is tailored to a specific goal, such as screening many factors or optimizing a few critical ones.

The historical use of the OFAT methodology is rooted in its simplicity and accessibility, and it can yield functional results in simple systems with minimal factor interactions. However, for the complex, multivariate systems typical of modern organic synthesis and drug development, its inherent limitations—particularly the failure to capture interaction effects, its gross inefficiency, and its inability to locate a true global optimum—render it obsolete. The paradigm shift towards Design of Experiments is justified by a compelling body of evidence. DoE provides a structured, statistically rigorous framework that delivers superior optimization outcomes with a more efficient use of precious resources. For researchers committed to rigorous and efficient scientific discovery, embracing and mastering DoE is not merely an option but a professional necessity.

In the pursuit of innovation within organic synthesis and drug development, the methodology for optimizing reaction conditions stands as a critical determinant of efficiency and success. For decades, the One-Factor-At-a-Time (OFAT) approach has been the ubiquitous, intuition-driven training in synthetic laboratories [3]. This method involves systematically varying a single parameter while holding all others constant, an process that is straightforward but inherently flawed for complex, multifactorial systems. In contrast, Design of Experiments (DoE) represents a fundamental shift towards a systematic, statistical framework that actively explores interactions between multiple variables simultaneously [13] [27]. This whitepaper argues that for modern research involving complex pathways—such as multi-step syntheses for pharmaceuticals or functional materials—transitioning from OFAT to DoE is not merely beneficial but essential. The core thesis is that DoE provides a robust, data-driven foundation for understanding complex systems, ultimately accelerating discovery, improving resource efficiency, and yielding more reliable and optimized outcomes where OFAT falls short [8].

The Critical Limitations of the OFAT Approach

The OFAT method, while useful for simple reactions with linear pathways, reveals significant deficiencies when applied to complex organic systems.

  • Inefficiency and Inaccuracy: OFAT requires investigating every possible combination of parameters independently, leading to an exponential growth in required experiments. This process is "sometimes inaccurate and inefficient to achieve optimization in a real sense" [3]. It fails to account for interactions between factors, meaning the true optimum condition, often residing in the interplay of variables, can be easily missed.
  • Inability to Model Interactions: The most significant flaw of OFAT is its blindness to factor interactions. In complex organic reactions, the effect of changing temperature may depend entirely on the solvent or catalyst used. OFAT cannot detect or quantify these critical interactions, leading to suboptimal conclusions and a poor understanding of the reaction landscape.
  • High Resource Burden: The trial-and-error nature of OFAT, reliant on chemist intuition, consumes disproportionate amounts of time, valuable starting materials, and laboratory resources, especially as the number of relevant variables increases.

The DoE Framework: A Systematic Foundation for Complex Systems

DoE is a class of statistical methods designed to construct a model that relates input parameters to desired outputs (e.g., yield, purity, device performance) [3]. Its principles directly address the shortcomings of OFAT:

  • Multifactorial Exploration: DoE is designed to vary multiple factors simultaneously according to a structured plan (e.g., factorial or fractional factorial designs). This allows for the efficient estimation of both main effects and, crucially, interaction effects between factors [27].
  • Structured Efficiency: Through principles like randomization, replication, and blocking, DoE ensures reliable, statistically sound results while minimizing the number of required experimental runs [28]. Screening designs, such as Plackett-Burman or definitive screening designs, are specifically tailored to efficiently identify the most influential variables from a large set, saving considerable resources [27].
  • Model-Based Prediction: The outcome of a well-executed DoE is a predictive model (often a polynomial response surface) of the system. This model allows researchers to understand the relationship between factors, visualize the response landscape, and pinpoint optimal regions with a degree of confidence impossible with OFAT.

Table 1: Core Quantitative Comparison Between OFAT and DoE Methodologies

Aspect One-Factor-At-a-Time (OFAT) Design of Experiments (DoE) Source / Implication
Experimental Efficiency Low; requires testing all combinations of levels. Number of runs = Π (Levels for each factor). High; uses structured arrays to maximize information. Runs can be a fraction of full factorial. [3] [27]
Ability to Detect Interactions None. Cannot quantify how one factor's effect changes with another's level. Explicitly models and quantifies 2-factor and higher-order interactions. [13] [27]
Underlying Approach Intuition-based, sequential trial-and-error. Statistical, model-based, and parallel. [3] [8]
Optimal Solution Reliability Low; may find local, not global, optimum due to ignored interactions. High; maps the response surface to identify robust optima. [13] [8]
Best Application Context Simple systems with 1-2 known critical variables and negligible interactions. Complex systems with multiple variables where interactions are suspected. [13] [27]

Case Study in Integration: DoE + Machine Learning for "From-Flask-to-Device" Optimization

A seminal example of DoE's power in complex systems is its integration with machine learning (ML) for optimizing organic light-emitting device (OLED) performance directly from reaction conditions, bypassing traditional purification [13]. This "from-flask-to-device" approach illustrates the paradigm shift.

Experimental Objective: To correlate the conditions of a Yamamoto macrocyclization reaction (producing a mixture of methylated [n]cyclo-meta-phenylenes) directly with the external quantum efficiency (EQE) of a fabricated OLED, eliminating separation steps.

Detailed Experimental Protocol (DoE + ML Workflow):

  • Factor & Level Selection: Five reaction factors were identified: equivalent of Ni(cod)2 (M), addition time (T), final concentration (C), % content of bromochlorotoluene (R), and % content of DMF in solvent (S). Each was assigned three levels [13].
  • DoE Matrix Construction: An L18 (2^1 × 3^7) Taguchi orthogonal array was selected to cover the 5-factor, 3-level design space with only 18 experimental runs [13].
  • Execution & Data Collection: The 18 reactions were performed under the specified conditions. The crude mixtures were minimally worked up and used directly to fabricate double-layer OLEDs. The EQE of each device was measured in quadruplicate [13].
  • Machine Learning Model Training: The dataset of 18 data points linking (M, T, C, R, S) to EQE was used to train three ML models: Support Vector Regression (SVR), Partial Least Squares Regression (PLSR), and Multilayer Perceptron (MLP) [13].
  • Model Validation & Prediction: Models were evaluated via leave-one-out cross-validation (LOOCV). The SVR model showed the lowest mean squared error (MSE = 0.0368) and was selected. It was used to generate a predictive heatmap across the five-dimensional parameter space [13].
  • Validation & Outcome: The SVR model predicted an optimal EQE of 11.3% at specific conditions. A validation experiment at those conditions yielded an EQE of 9.6 ± 0.1%, confirming the model's predictive power and surpassing the performance of devices made from purified materials (~0.9% EQE) [13].

Table 2: Quantitative Results from OLED Optimization Case Study [13]

Metric Value / Outcome Significance
DoE Runs 18 experiments (L18 array) Efficiently explored 5 factors at 3 levels each.
Best ML Model Support Vector Regression (SVR) Selected based on lowest LOOCV MSE (0.0368).
Predicted Optimal EQE 11.3% Identified via grid search on SVR model.
Experimentally Validated EQE 9.6% ± 0.1% Confirmed model accuracy and optimal condition.
EQE using Purified Materials ~0.9% Highlighted superiority of the DoE-optimized crude mixture.

Visualizing the Methodological Shift

The following diagrams, generated using DOT language, illustrate the logical and procedural differences between OFAT and DoE, as well as the integrated DoE+ML workflow.

OFAT_Workflow Start Define Reaction & Objective F1 Fix all factors at baseline Start->F1 OFAT_Loop Vary Factor 1 across levels F1->OFAT_Loop Record1 Record Response OFAT_Loop->Record1 F2 Set Factor 1 to its 'best' level Record1->F2 OFAT_Loop2 Vary Factor 2 across levels F2->OFAT_Loop2 Record2 Record Response OFAT_Loop2->Record2 End Declare Optimum (Potentially Flawed) Record2->End

OFAT Sequential Process

DOE_Workflow Start Define Factors, Levels & Objective Design Select Statistical Design (e.g., Factorial, Screening) Start->Design Matrix Generate Experimental Run Matrix Design->Matrix Execute Execute All Runs in Randomized Order Matrix->Execute Model Build Statistical Model (Main Effects + Interactions) Execute->Model Analyze Analyze Response Surface & Identify Optimum Region Model->Analyze Validate Confirm Optimum with Validation Runs Analyze->Validate

DoE Parallel Model-Based Process

DOE_ML_Integration Start Define System (Factors & Response) InitialDOE Initial DoE (Screening/Optimization) Start->InitialDOE Data Experimental Data (Inputs & Outputs) InitialDOE->Data Train Train Machine Learning Model Data->Train Model Predictive ML Model (e.g., SVR, Gaussian Process) Train->Model Suggest Model Suggests Next Most Informative Experiment Model->Suggest Loop Iterative Loop Suggest->Loop New Data Loop->Data Update Validate Validate Final Predicted Optimum Loop->Validate Stop Criteria Met

DoE+ML Adaptive Optimization Loop

The Scientist's Toolkit: Essential Reagents & Materials for DoE-Driven Synthesis

The following table details key research reagents and solutions central to the featured OLED case study and broadly applicable in DoE-driven organic synthesis optimization.

Table 3: Key Research Reagent Solutions for DoE in Organic Synthesis

Item / Reagent Function / Role in Optimization Example from Case Study [13]
Taguchi Orthogonal Arrays Pre-defined statistical matrices that allow balanced, efficient testing of multiple factors at multiple levels with minimal runs. L18 array used to design 18 experiments for 5 factors at 3 levels.
DoE Software (JMP, Minitab, etc.) Tools to design experiments, randomize run order, analyze results, fit models, and visualize response surfaces. Used for generating and analyzing the initial experimental design.
Machine Learning Platforms (Python/scikit-learn) Environments for building predictive models (SVR, PLSR, MLP) from DoE data to enable interpolation and optimization. SVR model trained to predict EQE from reaction conditions.
Automated Reactor/Sampling Systems Enables precise control over reaction parameters (time, temp, addition) and automated sampling for high-throughput data generation. Critical for executing the DoE matrix consistently and for self-optimization setups.
High-Throughput Analytics (HPLC, GC-MS) Rapid analytical techniques to quantify yields, purity, or product distribution for many samples generated by a DoE. MALDI-MS used to analyze product distribution in macrocyclization.
Nickel(0) Catalyst (e.g., Ni(cod)â‚‚) Transition metal catalyst for cross-coupling reactions; a critical factor whose loading is optimized. Factor M: Equivalent of Ni(cod)â‚‚ in Yamamoto macrocyclization.
Mixed Halide Substrates Starting materials where halide ratio can influence reaction kinetics and product distribution. Factor R: % content of bromochlorotoluene in substrate 1.
Solvent Blends Mixed solvent systems used to tune reaction environment, solubility, and kinetics. Factor S: % content of DMF in solvent mixture.
3-Oxo-delta4-chenodeoxycholyl-CoA3-Oxo-delta4-chenodeoxycholyl-CoA, MF:C45H70N7O19P3S, MW:1138.1 g/molChemical Reagent
9-Hydroxypentadecanoyl-CoA9-Hydroxypentadecanoyl-CoA, MF:C36H64N7O18P3S, MW:1007.9 g/molChemical Reagent

The transition from OFAT to DoE represents more than a change in technique; it is a fundamental shift towards a data-centric, systems-thinking philosophy in research. For professionals in organic synthesis and drug development, where systems are inherently complex and resources precious, this shift is crucial. DoE provides a rigorous framework to efficiently decode multifactorial interactions, build predictive models, and arrive at robust, high-performing solutions. When augmented with machine learning—creating an adaptive, iterative optimization loop—its power is magnified, potentially reducing experimental burden by 50-80% compared to conventional approaches [8]. As demonstrated in the "from-flask-to-device" optimization, this integrated methodology can unlock novel, high-performance materials and processes that traditional, sequential methods would never reveal. Embracing DoE is, therefore, an indispensable step in advancing scientific innovation and maintaining competitive edge in modern research.

Implementing DoE in the Lab: A Step-by-Step Workflow for Synthetic Chemists

In organic synthesis research, the journey from a conceptual molecule to a successfully synthesized compound is paved with critical decisions made at the experimental design stage. The foundational choice between One-Factor-at-a-Time (OFAT) and Design of Experiments (DoE) methodologies fundamentally shapes the efficiency, reliability, and ultimate success of research outcomes. While OFAT represents the traditionally taught approach—varying one factor while holding all others constant—modern complex chemical systems increasingly reveal its limitations in capturing the interactive effects that govern synthetic outcomes [6] [2]. This guide provides a structured framework for researchers to strategically define experimental goals and select factors within the context of DoE versus OFAT approaches, enabling more efficient navigation of multi-dimensional parameter spaces in organic synthesis and drug development.

The paradigm is steadily shifting toward DoE, particularly as high-throughput experimentation (HTE) and machine learning transform reaction optimization [29]. This transition is especially critical in pharmaceutical development, where flawed experimental approaches contribute significantly to drug candidate failures [30]. By establishing clear experimental goals and strategic factor selection from the outset, researchers can avoid the "blank spots" in experimental space that plague OFAT approaches and instead build comprehensive models that capture the true complexity of chemical systems.

Understanding OFAT and DoE: Core Principles and Comparative Analysis

One-Factor-at-a-Time (OFAT) Approach

OFAT, also known as One Variable at a Time (OVAT), represents the classical experimental approach wherein researchers examine the effect of a single factor while maintaining all other parameters at constant levels [2]. The procedural sequence involves: (1) establishing baseline conditions for all factors; (2) selecting one factor to vary across its range of interest; (3) measuring responses while keeping other factors rigidly fixed; (4) returning the varied factor to baseline before investigating the next factor; and (5) repeating this process sequentially for all factors of interest [2].

This method gained historical prominence due to its straightforward implementation and intuitive interpretation, requiring no advanced statistical knowledge for initial execution [2]. In traditional laboratory settings, OFAT aligned well with manual experimentation practices where physical setup modifications made simultaneous factor changes practically challenging. However, this apparent simplicity masks fundamental limitations in capturing the complexity of modern chemical synthesis.

Design of Experiments (DoE) Methodology

DoE represents a systematic, statistically-grounded framework for simultaneously investigating multiple factors and their interactions [2]. Rooted in principles of randomization, replication, and blocking, DoE employs structured experimental designs—such as factorial, response surface, and screening designs—to efficiently explore complex factor spaces [2] [31].

The fundamental advantage of DoE lies in its ability to decouple individual factor effects from their interactions through carefully constructed experimental arrays. Rather than exploring a single dimensional axis at a time, DoE investigates points across the entire experimental space, enabling researchers to build mathematical models that predict responses for any factor combination within the studied ranges [31]. This approach has become increasingly accessible through specialized software platforms that facilitate design generation and statistical analysis.

Comparative Analysis: OFAT versus DoE

Table 1: Fundamental characteristics of OFAT and DoE approaches

Characteristic OFAT DoE
Factor Variation Sequential Simultaneous
Interaction Detection Cannot detect interactions Explicitly models interactions
Experimental Efficiency Low (requires many runs) High (maximizes information per run)
Statistical Foundation Limited Robust (randomization, replication, blocking)
Model Building Capability Limited to individual factors Comprehensive mathematical models
Optimization Approach Local optimization along single dimensions Global optimization across design space
Resource Utilization Inefficient use of resources Efficient resource allocation

Table 2: Advantages and disadvantages of OFAT and DoE

OFAT DoE
Advantages Advantages
• Widely taught and understood [6] • Systematic coverage of experimental space [6]
• Straightforward implementation [6] • Efficient resource use [6] [2]
• Simple interpretation for single factors • Identifies interaction effects [2]
• Enables mathematical modeling of responses [31]
Disadvantages Disadvantages
• Limited coverage of experimental space [6] • Minimum entry barrier of approximately 10 experiments [6]
• Fails to identify interactions [6] [2] • May require experiments anticipated to "fail" [6]
• May miss optimal solutions [6] • Requires statistical knowledge for implementation
• Inefficient use of resources [6] [2] • Initial learning curve for experimental design

The critical limitation of OFAT emerges most prominently in its inability to detect factor interactions, which are fundamental to complex chemical systems [2]. Simulation studies demonstrate that OFAT finds the true process optimum only 20-30% of the time, even in simple two-factor systems [32]. This statistical blindness comes with significant resource costs—a process with 5 continuous factors requires 46 experimental runs using OFAT, while an equivalent DoE can characterize the same space in just 12-27 runs [32].

Defining Experimental Goals in Organic Synthesis

Aligning Goals with Methodological Selection

The strategic selection between OFAT and DoE begins with precise articulation of experimental goals. Different objectives in organic synthesis demand distinct methodological approaches, with OFAT retaining limited applicability for simple characterizations, while DoE delivers superior performance for optimization and modeling tasks.

Preliminary Factor Screening: In early exploratory stages where the objective is identifying influential factors from a large candidate set, DoE screening designs (e.g., fractional factorials, Plackett-Burman) provide dramatically superior efficiency. While OFAT might theoretically screen factors sequentially, it risks missing critical interactions and requires substantially more experimental runs [2].

Reaction Optimization: For optimizing yield, selectivity, or other critical responses, DoE unequivocally outperforms OFAT. The simultaneous factor variation in DoE enables researchers to model response surfaces and locate optimal conditions, including complex interactive effects that OFAT cannot detect [2] [32]. Pharmaceutical industry reports indicate DoE reduces assay development timelines by 30-70% compared to OFAT approaches [30].

Robustness Testing: When establishing operational ranges for process robustness, DoE provides comprehensive understanding of factor effects across the design space, whereas OFAT only characterizes individual factor axes, potentially missing failure modes that occur from specific factor combinations [2].

Reaction Discovery: Emerging applications of HTE combined with DoE principles enable accelerated reaction discovery by broadly exploring chemical space [14]. While OFAT relies heavily on serendipity and researcher intuition, structured experimental designs systematically probe diverse condition combinations, increasing opportunities for novel reactivity discovery.

Experimental Goal Framework

G Start Define Experimental Objectives GoalType Classify Primary Goal Start->GoalType Screening Factor Screening (Rapid identification of influential factors) GoalType->Screening Identify influential factors Optimization Process Optimization (Finding optimal conditions across multiple responses) GoalType->Optimization Optimize multiple responses Modeling System Modeling (Understanding factor effects and interactions) GoalType->Modeling Understand system behavior Robustness Robustness Testing (Establishing operable ranges and failure boundaries) GoalType->Robustness Establish process robustness ScreenMethod Recommended: DoE Screening Designs (Fractional Factorial, Plackett-Burman) Screening->ScreenMethod OFATLimited OFAT Application Limited to: - Simple system characterization - Single factor effect demonstration - Educational purposes Screening->OFATLimited OptimMethod Recommended: DoE Optimization Designs (Response Surface Methodology, Central Composite Designs) Optimization->OptimMethod Optimization->OFATLimited ModelMethod Recommended: DoE Modeling Designs (Full Factorial, D-Optimal) Modeling->ModelMethod Modeling->OFATLimited RobustMethod Recommended: DoE Robustness Designs (Factorial with center points, Custom Designs) Robustness->RobustMethod Robustness->OFATLimited

Experimental Goal Classification and Methodology Selection Workflow

Strategic Factor Selection for Effective Experimentation

Categorizing Factor Types

Strategic factor selection begins with comprehensive categorization of potential variables that may influence the synthetic process. In organic synthesis, factors typically fall into three primary classifications:

Continuous Factors: These variables span a measurable range and can be set to any value within operational limits. Examples include temperature (°C), concentration (mol/L), reaction time (hours), catalyst loading (mol%), and pressure (atm). Continuous factors are ideally suited for response surface modeling and optimization in DoE, whereas OFAT tests only discrete points along these continua.

Categorical Factors: These variables represent distinct states or types rather than numerical values. Common categorical factors in organic synthesis include solvent type (DMSO, THF, MeCN), catalyst identity (Pd(PPh₃)₄, Pd(dba)₂, Ni(COD)₂), ligand class (phosphine, amine, N-heterocyclic carbene), and substrate class (aryl halides, alkyl halides). DoE handles categorical factors efficiently through structured designs, while OFAT requires complete re-optimization for each category.

Process Parameters: These factors relate to experimental execution rather than chemical composition, including addition rate (slow/fast), mixing intensity (RPM), order of addition, and quenching method. Such parameters often exhibit significant interactions with chemical factors, making them particularly poorly suited for OFAT investigation.

Factor Selection Methodology

The process of selecting factors for experimental design follows a structured approach:

  • Brainstorming Phase: Compile an exhaustive list of potentially influential factors through literature review, mechanistic considerations, and experimental observation. At this stage, inclusivity is preferable to premature exclusion.

  • Preliminary Risk Assessment: Classify each factor based on prior knowledge and mechanistic understanding into high, medium, and low influence categories. This assessment guides strategic allocation of experimental resources.

  • Factor Prioritization: Apply the Pareto principle to identify the vital few factors that likely account for the majority of response variation. Techniques such as cause-and-effect diagrams and failure mode effects analysis can support this prioritization.

  • Experimental Design Integration: Select the appropriate experimental design based on the number and type of prioritized factors. Screening designs efficiently handle large factor sets (8-20 factors), while optimization designs focus on detailed characterization of critical factors (3-6 factors).

Research Reagent Solutions for Organic Synthesis Experimentation

Table 3: Essential research reagents and materials for organic synthesis experimentation

Reagent/Material Function in Experimental Design Application Notes
Catalyst Libraries Systematic variation of catalyst identity and loading Enable categorical factor screening; particularly valuable in transition-metal catalyzed reactions
Solvent Suites Investigation of solvent effects on reaction outcome Cover diverse polarity, coordination, and protic/aprotic characteristics
Substrate Arrays Evaluation of substrate scope and generality Designed with systematic electronic and steric variation
Additive Sets Identification of beneficial additives for yield or selectivity improvement Include bases, acids, salts, and ligands in structured arrays
High-Throughput Experimentation Platforms Miniaturization and parallelization for efficient condition screening [14] Enable testing of hundreds to thousands of conditions with minimal reagent consumption
Automated Synthesis Systems Standardization and reproducibility of experimental execution [14] Reduce operational variability, especially valuable for reaction discovery

Implementing DoE: Practical Protocols for Organic Synthesis

Preliminary Screening Designs

For initial factor screening where the objective is identifying influential factors from a larger set, two-level fractional factorial designs provide maximum efficiency. The implementation protocol includes:

  • Design Specification: Select 6-12 potentially influential factors for initial screening. For 6 factors, a resolution IV fractional factorial design (2^(6-1)) requiring 32 experimental runs preserves the ability to detect all main effects unconfounded by two-factor interactions.

  • Factor Range Selection: Establish scientifically reasonable ranges for each factor based on literature precedent and mechanistic considerations. Wider ranges increase effect detection power but must remain within operational limits.

  • Randomization Protocol: Execute experimental runs in computer-generated random order to mitigate confounding from lurking variables and time-dependent effects [2].

  • Response Measurement: Quantify critical responses for each run, typically including conversion, yield, and selectivity metrics. Analytical methods should provide sufficient precision to detect meaningful differences.

  • Statistical Analysis: Apply analysis of variance (ANOVA) to identify statistically significant factors (p < 0.05) and model the relationship between factors and responses.

Response Surface Methodology for Optimization

For detailed optimization of critical factors identified through screening, Response Surface Methodology (RSM) provides comprehensive characterization:

  • Experimental Design Selection: Central Composite Designs (CCD) or Box-Behnken Designs (BBD) efficiently model quadratic response surfaces. For 3 factors, a CCD requires 20 runs (8 factorial points, 6 axial points, 6 center points), while a BBD requires 15 runs.

  • Model Development: Fit second-order polynomial models to experimental data using regression analysis. The general form for three factors is: Y = β₀ + β₁X₁ + β₂Xâ‚‚ + β₃X₃ + β₁₂X₁Xâ‚‚ + β₁₃X₁X₃ + β₂₃Xâ‚‚X₃ + β₁₁X₁² + β₂₂X₂² + β₃₃X₃²

  • Optimization Analysis: Utilize numerical optimization algorithms or graphical response surface analysis to identify factor settings that simultaneously optimize all responses, often requiring compromise between competing objectives.

  • Validation Experiments: Confirm model predictions through additional experimental runs at identified optimum conditions, comparing predicted versus observed responses.

High-Throughput Experimentation Integration

The integration of HTE with DoE principles represents a paradigm shift in organic synthesis optimization [14]. The implementation workflow includes:

G Step1 Experimental Design (DoE matrix generation specifying factor combinations) Step2 Reagent Plate Preparation (Liquid handling automation for miniaturized reaction setup) Step1->Step2 Step3 Parallel Reaction Execution (Simultaneous experimentation under controlled conditions) Step2->Step3 Annotation1 HTE enables testing of 384-1536 reactions simultaneously [14] Step2->Annotation1 Step4 High-Throughput Analysis (Parallel analytical measurement via LC-MS, GC-MS, or NMR) Step3->Step4 Step5 Data Processing (Automated data extraction and response calculation) Step4->Step5 Step6 Model Building & Optimization (Statistical analysis and predictive model development) Step5->Step6 Step7 Validation & Iteration (Confirmatory experiments and design augmentation) Step6->Step7 Annotation2 Machine learning algorithms enhance model prediction from HTE data [29] Step6->Annotation2 Step7->Step1 Iterative refinement

High-Throughput Experimentation Workflow Integrated with DoE Principles

The methodological transition from OFAT to DoE represents a fundamental evolution in experimental strategy for organic synthesis research. While OFAT retains limited applicability for simple educational demonstrations or single-factor effect characterization, its systematic failures in detecting interactions and locating true optima render it inadequate for modern research challenges [32]. The integration of DoE with emerging technologies—particularly high-throughput experimentation and machine learning—creates unprecedented opportunities for accelerated reaction discovery, optimization, and understanding [29] [14].

For researchers embarking on experimental programs in organic synthesis or drug development, the strategic framework presented in this guide enables informed decisions about goal definition and factor selection. By embracing systematic experimentation approaches, the scientific community can overcome the limitations of traditional methods that contribute to high failure rates in drug discovery and lengthy development timelines [30]. The future of organic synthesis lies in strategic experimental design that efficiently extracts maximum information from minimal resources while capturing the complex reality of chemical systems.

In organic synthesis research, the traditional One-Factor-at-a-Time (OFAT) approach has been widely used for process optimization. This method involves altering a single variable while keeping all others constant, then repeating the process for subsequent variables [6] [23]. While straightforward and widely taught, OFAT presents significant limitations: it provides limited coverage of the experimental space, may miss optimal solutions, fails to identify interactions between factors, and represents an inefficient use of resources [6] [23]. Most critically, for systems where variables are not perfectly independent, the final combination of variable set points after an OFAT approach is likely to be suboptimal, with the degree of suboptimality depending on the order in which variables were perturbed [23].

Design of Experiments (DoE) provides a powerful statistical alternative that systematically investigates multiple factors simultaneously [6]. This approach is particularly valuable in complex domains such as drug development and organic synthesis, where multiple factors often interact in non-linear ways. Within the DoE framework, screening designs (particularly fractional factorials) and optimization designs (notably Response Surface Methodology) serve distinct but complementary purposes in a structured experimental campaign [33] [34]. This guide examines the strategic application of each design type within organic synthesis research, providing a structured framework for moving efficiently from initial factor identification to process optimization.

Core Concepts: Screening and Optimization Designs

The Sequential Nature of DoE

DoE is most effective when applied sequentially, with each experimental phase serving a specific purpose and informing the next [33] [34]. A typical campaign progresses through several stages:

  • Screening: Identifying the few critical factors from many potential candidates [35]
  • Refinement and Iteration: Studying interactions and narrowing optimal ranges [33]
  • Optimization: Modeling quadratic effects and locating optimal settings [35]
  • Robustness Testing: Determining process sensitivity to factor variations [33]

This sequential approach contrasts sharply with OFAT, allowing researchers to learn rapidly throughout the experimental process rather than committing to a single comprehensive experimental plan [33].

Fractional Factorial Designs for Screening

Fractional factorial designs (FFDs) are specialized experimental plans that efficiently screen a large number of factors using a rational subset of the full factorial design space [33] [23]. They are predicated on the sparsity-of-effects principle – the assumption that while there may be many potential effects, only a few are importantly large, and that main effects and lower-order interactions (between 2-3 factors) are more influential than complex higher-order interactions [33].

FFDs achieve efficiency through aliasing (or confounding), where certain effects cannot be distinguished from one another [33]. By strategically aliasing higher-order interactions (which are presumed negligible) with potential main effects and two-factor interactions, FFDs dramatically reduce the required experimental runs while still providing reliable information about the most important effects [33]. The resolution of a fractional factorial design indicates its ability to separate effects of different orders, with higher resolutions providing clearer separation between main effects and low-order interactions [33].

Response Surface Methodology for Optimization

Response Surface Methodology (RSM) comprises statistical techniques for modeling and analyzing problems where several independent variables influence a dependent variable or response, with the goal of optimizing this response [36]. Unlike screening designs which typically use two levels per factor, RSM employs at least three levels to detect and model curvature in the response, enabling the identification of optimal conditions within the experimental region [33] [36].

The most common RSM designs include Central Composite Designs (CCD) and Box-Behnken Designs (BBD) [23] [36]. These designs efficiently estimate the coefficients of a quadratic polynomial model that describes how factors influence the response, allowing researchers to locate maxima, minima, or saddle points in the response surface [36].

Comparative Analysis: Key Differences and When to Use Each Design

The table below summarizes the fundamental distinctions between fractional factorial and response surface designs:

Table 1: Comparative Analysis of Screening vs. Optimization Designs

Characteristic Screening (Fractional Factorial) Designs Optimization (RSM) Designs
Primary Objective Identify vital few factors from many candidates [35] [34] Model nonlinear relationships and locate optimal conditions [35] [36]
Experimental Stage Early-phase investigation [33] Late-phase optimization [33]
Factor Levels Typically 2 levels per factor [33] Minimum 3 levels per factor [33]
Model Complexity Main effects and limited interactions [33] Full quadratic models with curvature [36]
Key Assumption Sparsity of effects (few important factors) [33] Presence of curvature near optimum [33]
Aliasing/Confounding Higher-order interactions confounded with main effects [33] All main effects clear of two-factor interactions [35]
Run Efficiency High efficiency for factor screening [33] More runs required but sufficient for quadratic model [33]

The strategic relationship between these designs is sequential, as visualized in the following experimental workflow:

Practical Implementation Guide

Executing Fractional Factorial Screening Designs

Step 1: Design Setup and Selection Begin by identifying all potential factors that might influence your synthetic process, including categorical factors (e.g., catalyst type, solvent composition) and continuous factors (e.g., temperature, concentration, reaction time) [23]. Select appropriate high and low levels for each factor based on practical constraints and scientific knowledge. Choose a fractional factorial design with sufficient resolution to separate effects of interest; Resolution IV designs are often appropriate as they prevent confounding of main effects with two-factor interactions [33] [35].

Step 2: Experimental Execution and Data Collection Execute experimental runs in randomized order to minimize confounding from uncontrolled variables [33]. The example below demonstrates a real-world application from nanomaterials synthesis:

Table 2: Fractional Factorial Application in h-BN Coating Synthesis

Study Objective Factors Investigated Responses Measured Key Findings
Optimize h-BN coating synthesis for antibiofilm applications [37] Precursor mass, Growth time, Substrate conditioning, Applied voltage, Medium concentration [37] Surface roughness, Wettability [37] Precursor mass and medium concentration most significantly influenced surface roughness [37]

Step 3: Statistical Analysis and Model Interpretation Analyze data using statistical software to identify significant main effects and interactions. Create Pareto charts and normal probability plots to visually identify effects that stand out from noise. Remember that effects are partially confounded in fractional factorial designs, so interpretation requires scientific judgment alongside statistical results [33] [35].

Implementing Response Surface Methodology

Step 1: Design Selection and Setup Based on screening results, select the most critical 2-4 factors for optimization. Choose an appropriate RSM design - Central Composite Designs (CCD) are popular for their flexibility, while Box-Behnken Designs (BBD) offer efficiency with fewer runs [36]. The experimental region should encompass the suspected optimum based on screening results.

Step 2: Experimental Execution RSM requires more runs than screening designs but remains efficient compared to OFAT. A typical CCD for 3 factors requires 15-20 experiments, while a comparable OFAT approach might require many more [36]. Include center points to estimate pure error and check for curvature.

Step 3: Model Development and Optimization Fit a quadratic model to the experimental data. The general form for a quadratic model with k factors is [36]:

[Y = \beta0 + \sum{i=1}^k \betai Xi + \sum{i=1}^k \beta{ii} Xi^2 + \sum{i{ij} Xi X_j + \varepsilon]}>

Where Y is the predicted response, β₀ is the constant coefficient, βi are linear coefficients, βii are quadratic coefficients, βij are interaction coefficients, and ε represents error.

Use analysis of variance (ANOVA) to assess model significance and lack-of-fit. Once a satisfactory model is obtained, use contour plots and response surface plots to visualize the relationship between factors and responses, then identify optimal conditions [36].

Case Study: Organic Matter Removal Optimization

A comprehensive study on natural organic matter removal from aqueous solutions using advanced oxidation processes (UV/Hâ‚‚Oâ‚‚) demonstrates the sequential application of screening followed by RSM [36]. Researchers first identified critical factors through preliminary experiments, then applied a Box-Behnken design to optimize four key parameters: Hâ‚‚Oâ‚‚ concentration (100-180 mg/L), pH (3-11), reaction time (10-30 min), and initial TOC concentration (4-10 mg/L) [36].

Table 3: Response Surface Methodology Experimental Results

Run Order Hâ‚‚Oâ‚‚ (mg/L) pH Time (min) Initial TOC (mg/L) TOC Removal (%)
1 [36] 180 7 20 4 84
2 [36] 180 7 30 7 80

Through response surface analysis, researchers developed a quadratic model with R² = 0.98, indicating excellent fit to experimental data [36]. The model revealed that increasing H₂O₂ concentration and reaction time improved TOC removal, while neutral to slightly acidic pH values were optimal. The optimized conditions were H₂O₂ concentration of 100 mg/L, pH 6.12, reaction time 22.42 min, and initial TOC concentration of 4 mg/L, achieving 78.02% predicted TOC removal with experimental confirmation of 76.50% [36]. This demonstrates RSM's effectiveness for process optimization in complex chemical systems.

Advanced Concepts and Modern Alternatives

Definitive Screening Designs

Definitive Screening Designs (DSDs) represent a modern innovation that combines aspects of both screening and optimization designs [35]. These three-level designs enable researchers to screen many factors while simultaneously detecting curvature and estimating quadratic effects [35]. Key advantages of DSDs include:

  • All main effects are clear of any aliasing with two-factor interactions [35]
  • Ability to estimate two-factor interactions with partial confounding [35]
  • Requirement of only one more run than twice the number of factors being studied [35]
  • Potential to skip traditional screening and proceed directly to optimization for simpler systems [35]

However, DSDs have lower statistical power for detecting quadratic effects compared to dedicated RSM designs and require more complex analysis approaches, often utilizing stepwise regression due to the fully saturated nature of the designs [35].

The Scientist's Toolkit: Essential Research Reagents and Materials

Successful implementation of DoE in organic synthesis requires careful selection of reagents and materials. The table below outlines key categories:

Table 4: Essential Research Reagents and Materials for DoE Studies

Reagent/Material Function in DoE Studies Application Examples
Amino Borane (BH₆N) [37] CVD precursor for 2D material synthesis h-BN coating production for antibiofilm applications [37]
Hydrogen Peroxide [36] Oxidizing agent in advanced oxidation processes Natural organic matter removal from water [36]
Polymethyl Methacrylate (PMMA) [37] Polymer support for electrochemical transfer h-BN coating transfer to substrates [37]
Sodium Hydroxide [37] Electrolyte for electrochemical processes Transfer process for 2D materials [37]
(R)-3-hydroxystearoyl-CoA(R)-3-hydroxystearoyl-CoA, MF:C39H70N7O18P3S, MW:1050.0 g/molChemical Reagent
13-hydroxyhexadecanoyl-CoA13-hydroxyhexadecanoyl-CoA, MF:C37H66N7O18P3S, MW:1021.9 g/molChemical Reagent

Strategic selection between screening and optimization designs is fundamental to efficient experimental work in organic synthesis and drug development. Fractional factorial designs provide unparalleled efficiency for identifying critical factors from many candidates, while Response Surface Methodology offers powerful capabilities for modeling complex relationships and locating optimal conditions. When deployed sequentially within a structured experimental campaign, these methods dramatically outperform traditional OFAT approaches in both efficiency and effectiveness, enabling researchers to navigate complex experimental spaces and develop robust, optimized processes with minimal experimental investment. The modern experimentalist should view these approaches not as competing alternatives but as complementary tools in a comprehensive strategy for process understanding and optimization.

Central Composite and Box-Behnken Designs for Modeling Curvature

In organic synthesis research, the traditional method for optimizing reactions has long been the One-Factor-at-a-Time (OFAT) approach. While intuitively simple, OFAT varies one parameter while holding all others constant, fundamentally ignoring interactions between factors and often leading to suboptimal results and inefficient resource use [4]. In contrast, Design of Experiments (DoE) provides a systematic, statistical framework for simultaneously investigating multiple factors and their complex interactions [38]. Within DoE, Response Surface Methodology (RSM) is a powerful collection of mathematical and statistical techniques used for modeling and optimizing processes when the response of interest is influenced by several variables [39]. RSM is particularly valuable for mapping a region of a response surface, understanding how variable changes affect the response, and finding factor levels that optimize the response [40].

A critical limitation of two-level factorial designs is their inability to detect curvature in response surfaces. When a process is near its optimum, the response surface often exhibits curvature, which requires more complex modeling than simple planar surfaces [41]. Central Composite Design (CCD) and Box-Behnken Design (BBD) are two principal RSM designs specifically developed to address this limitation by efficiently estimating curvature through quadratic terms, enabling researchers to locate optimal conditions with precision and reliability [41] [40].

Understanding Response Surface Designs

The Quadratic Model

Both CCD and BBD are designed to fit a full quadratic model, which extends linear models by adding squared terms to capture curvature. The general form of this second-order model is:

Y = β₀ + ∑βᵢXᵢ + ∑βᵢⱼXᵢXⱼ + ∑βᵢᵢXᵢ² + ε

Where:

  • Y is the predicted response
  • β₀ is the constant term
  • βᵢ are the coefficients for linear effects
  • βᵢⱼ are the coefficients for interaction effects
  • βᵢᵢ are the coefficients for quadratic effects
  • Xáµ¢ and Xâ±¼ are the coded independent variables
  • ε is the random error term [39]

This model can identify not just the direction and magnitude of factor effects, but also the presence of maxima or minima within the experimental region—critical information for optimization [25].

The Sequential Nature of RSM

A fundamental strength of RSM is its sequential approach to experimentation. The process typically begins with screening designs to identify influential factors, followed by steepest ascent/descent experiments to rapidly move toward the optimum region, and culminates with response surface designs like CCD or BBD to precisely model curvature and locate the optimum [25]. This iterative learning process allows researchers to efficiently converge on optimal conditions while building comprehensive process understanding.

Central Composite Design (CCD)

Structure and Components

The Central Composite Design builds upon factorial foundations by augmenting them with additional points to enable curvature estimation. A complete CCD consists of three distinct components:

  • Factorial Points: The corner points of the design space (coded as ±1) that form a factorial or fractional factorial design. These points estimate linear and interaction effects [41] [42].
  • Center Points: Multiple runs at the center of the design space (coded as 0) that provide an estimate of pure error and allow checking for curvature [41] [42].
  • Star Points (or axial points): Points extended beyond the factorial corners along each factor axis (coded as ±α) that enable estimation of quadratic effects [41] [42].

CCD_Structure F1 Factorial (-1,-1) F2 F1->F2 F4 F2->F4 F3 F3->F1 F4->F3 C Center (0,0) S1 Star (-α,0) C->S1 S2 C->S2 S3 C->S3 S4 C->S4

CCD Structure for Two Factors

Varieties of CCD

The value of α (the distance of star points from the center) determines the specific type of CCD, each with distinct properties and applications:

Type Terminology α Value Properties Application Context
Circumscribed CCC |α| > 1 Rotatable, requires 5 levels General optimization where extreme conditions beyond current range are feasible [42]
Inscribed CCI |α| < 1 Scaled to fit within cube, 5 levels When the factorial points are at the safe operational limits [42]
Face-Centered CCF α = ±1 3 levels, not rotatable When the current factor range represents absolute limits [40] [42]

For rotatable designs, the specific value of α is calculated as α = (2^k)^(1/4) for full factorial designs, where k is the number of factors [42].

Experimental Protocol for CCD

Implementation Workflow:

  • Begin with a factorial or resolution V fractional factorial design with center points [40].
  • Based on initial analysis indicating curvature, add star points to complete the CCD structure [41].
  • If necessary, divide the experiment into orthogonal blocks to account for nuisance variables (e.g., different batches of raw materials) [42].
  • Execute all experimental runs in randomized order to minimize confounding with external factors [4].
  • Fit the quadratic model and validate model adequacy through residual analysis and lack-of-fit tests [38].

Key Advantages:

  • Sequential Experimentation: CCD naturally supports building upon existing factorial experiments by adding star and center points [41] [40].
  • Rotatability: Properly designed CCD provides constant prediction variance at all points equidistant from the center [42].
  • Comprehensive Modeling: Estimates all main, interaction, and quadratic effects efficiently [39].

Box-Behnken Design (BBD)

Structure and Components

The Box-Behnken Design takes a fundamentally different structural approach. Instead of building upon factorial designs, BBD places experimental runs at the midpoints of the edges of the experimental space rather than at the corners [41]. For a three-factor system, this means the design points are located at the middle of each of the 12 edges of the cube, plus center points for estimating error [41].

BBD_Structure B1 Edge Point (-1,0) B2 B1->B2 B4 B2->B4 B3 B3->B1 B4->B3 C Center (0,0) C->B1 C->B2 C->B3 C->B4

BBD Structure for Two Factors

Key Characteristics

BBD possesses several distinctive characteristics:

  • No Extreme Corner Points: The design never tests conditions where all factors are simultaneously at their maximum or minimum values [41].
  • Strictly Within Boundaries: All experimental runs stay within the boundaries originally defined by the factor ranges [41].
  • Three Levels per Factor: Unlike CCD which can require up to five levels, BBD uses only three levels for each factor (low, middle, high) [40].
  • Efficient Run Count: BBD typically requires fewer runs than CCD with the same number of factors, making it more economical [40].
Experimental Protocol for BBD

Implementation Workflow:

  • Identify the factors and their ranges based on prior knowledge or screening experiments [41].
  • Select the appropriate BBD matrix for the number of factors [43].
  • Include sufficient center points (typically 3-6) to estimate pure error [41].
  • Execute all runs in randomized order [4].
  • Fit the quadratic model and check model adequacy using statistical measures (R², adjusted R², prediction R²) [38].
  • Use contour plots and response surface plots to visualize the relationship between factors and responses [43].

Key Advantages:

  • Run Efficiency: Fewer experimental runs required compared to CCD for the same number of factors [40].
  • Safety Considerations: Avoids potentially dangerous extreme conditions where all factors are at their limits [41].
  • Practical Implementation: All design points fall within safe operating zones, which is particularly valuable in chemical processes with constraints [40].

Comparative Analysis: CCD vs. BBD

Quantitative Comparison of Run Requirements

The choice between CCD and BBD significantly impacts experimental resource requirements. The table below compares the number of experimental runs required for different numbers of factors (assuming 3-6 center points for typical designs):

Number of Factors Box-Behnken Design Central Composite Design
3 15 17
4 27 27
5 43 45
6 63 79
7 87 145
8 115 275

Comparison of experimental run requirements for CCD and BBD [41]

The divergence in run count becomes particularly pronounced beyond six factors, making BBD significantly more efficient for experiments with many factors [41].

Qualitative Comparison and Selection Guidelines
Characteristic Central Composite Design Box-Behnken Design
Sequential Capability Excellent - can build on existing factorial designs [41] [40] Poor - requires complete commitment to full design [41]
Factor Levels 5 levels (CCC), 3 levels (CCF) [42] 3 levels per factor [40]
Extreme Conditions Tests all corners and may extend beyond [41] Avoids extreme combinations of all factors [41]
Rotatability Can be designed to be rotatable [42] Nearly rotatable for some designs [43]
Optimal Use Case Early-stage process understanding, sequential learning [41] Well-characterized systems with known important factors [41]
Safety Considerations May test beyond safe operating limits [40] All points within defined safe boundaries [40]

Applications in Organic Synthesis and Drug Development

Case Study: OLED Material Optimization

A recent study demonstrated the power of combining DoE with machine learning for optimizing reaction conditions in the synthesis of organic light-emitting device (OLED) materials. Researchers used a Taguchi orthogonal array design to efficiently explore five factors at three levels each with only 18 experimental runs [13]. The factors included equivalent of Ni(cod)â‚‚, dropwise addition time, final concentration, % content of bromochlorotoluene, and % content of DMF in solvent [13]. The resulting crude mixtures were directly used in OLED fabrication, eliminating energy-consuming purification steps. By augmenting the DoE data with machine learning predictions (support vector regression), the team successfully correlated reaction conditions with device performance and identified optimal conditions that achieved an external quantum efficiency of 9.6%, surpassing the performance of purified materials [13].

Cross-Coupling Reaction Screening

In pharmaceutical development, cross-coupling reactions are essential for constructing complex molecules. A 2025 study applied Plackett-Burman design to screen key factors in Mizoroki-Heck, Suzuki-Miyaura, and Sonogashira-Hagihara reactions [4]. The design efficiently evaluated five critical factors—electronic effect of phosphine ligands, Tolman's cone angle, catalyst loading, base strength, and solvent polarity—across only twelve experimental runs [4]. This approach enabled researchers to statistically rank factor importance and identify influential variables for each reaction type, providing a foundation for further optimization using response surface methodologies.

Typical Research Reagent Solutions
Reagent/Category Function in Optimization Application Example
Phosphine Ligands Modulate catalyst activity and selectivity Screening electronic and steric properties in cross-coupling reactions [4]
Palladium Catalysts Facilitate cross-coupling transformations Kâ‚‚PdClâ‚„, Pd(OAc)â‚‚ in Mizoroki-Heck, Suzuki-Miyaura reactions [4]
Solvent Systems Influence reaction kinetics and mechanism DMSO, MeCN with different polarities for solubility and reactivity modulation [4]
Base Additives Facilitate transmetalation and catalyst regeneration NaOH, Et₃N for adjusting reaction pH and promoting catalytic cycles [4]
Internal Standards Enable accurate reaction monitoring Dodecane for GC-MS quantification in cross-coupling optimization [4]

Implementation Workflow and Future Directions

Integrated DoE Workflow for Organic Synthesis

The modern approach to reaction optimization integrates multiple DoE strategies in a sequential workflow:

DOE_Workflow cluster_1 Factor Screening cluster_2 Optimization cluster_3 Advanced Modeling Start Define Optimization Objectives PBD Screening Design (Plackett-Burman) Start->PBD Factorial Factorial Design (Identify Interactions) PBD->Factorial SteepestAscent Steepest Ascent/Descent (Move to Optimum Region) Factorial->SteepestAscent RSM Response Surface Design (CCD or BBD) SteepestAscent->RSM Validation Model Validation (Confirmation Runs) RSM->Validation ML Machine Learning (Prediction & Refinement) Validation->ML

Integrated DoE Workflow for Synthesis Optimization

The future of reaction optimization lies in combining traditional DoE with modern machine learning (ML) approaches. As demonstrated in the OLED case study, ML can augment DoE by predicting optimal conditions across a broader parameter space than practical to test experimentally [13]. Current research focuses on:

  • Hybrid DoE-ML Frameworks: Using initial DoE data to train ML models that then guide subsequent experimentation [13].
  • Multi-Objective Optimization: Simultaneously optimizing multiple responses (yield, purity, cost, environmental impact) using desirability functions [3].
  • Automated Self-Optimization Systems: Integrating DoE with flow chemistry and real-time analytics for fully automated reaction optimization [3].

Central Composite and Box-Behnken designs represent sophisticated approaches for modeling curvature and locating optimal conditions in complex experimental systems. While both enable efficient estimation of quadratic response surfaces, they differ fundamentally in structure, implementation requirements, and practical applications. CCD's strength lies in its sequential nature and flexibility for exploring broader operational spaces, making it ideal for earlier-stage process understanding. BBD's advantage emerges in its run efficiency and inherent safety for well-characterized systems operating near constraints.

For organic synthesis researchers transitioning from OFAT to statistical approaches, both designs offer powerful capabilities for understanding complex reaction landscapes, optimizing multiple performance metrics simultaneously, and developing robust synthetic processes. The choice between them should be guided by specific experimental context, including prior process knowledge, safety constraints, resource availability, and optimization objectives. As the field advances, the integration of these traditional DoE approaches with machine learning and automation promises to further accelerate pharmaceutical development and reaction optimization.

In the competitive landscape of organic synthesis and drug development, the efficiency of research directly translates to strategic advantage. While the traditional one-factor-at-a-time (OFAT) approach offers intuitive appeal, its limitations in exploring complex, interactive chemical spaces are well-documented [13] [4]. The Design of Experiments (DoE) paradigm provides a statistically rigorous framework to overcome these limitations, systematically uncovering factor effects and interactions with minimal resource expenditure [4]. This guide details the core workflow of a DoE study, from initial design to final data collection, contextualized within the critical debate of DoE versus OFAT for optimizing complex organic syntheses and material development processes.

Core Principles: Contrasting DoE and OFAT Philosophies

The fundamental difference between OFAT and DoE lies in experimental philosophy and efficiency. OFAT varies a single factor while holding all others constant, inherently ignoring potential interactions between variables and often requiring a prohibitively large number of runs to explore a multi-dimensional space [4]. In contrast, DoE is a structured method for simultaneously investigating multiple factors and their interactions, allowing researchers to model the response surface and identify optimal conditions with far fewer experiments [13] [44] [4]. This is particularly crucial in systems like catalytic cross-coupling reactions or multi-step device fabrication, where factors such as ligand electronics, solvent polarity, and catalyst loading interact synergistically [13] [4].

Table 1: Quantitative Comparison of DoE and OFAT for a Hypothetical 3-Factor, 3-Level Study

Aspect One-Factor-at-a-Time (OFAT) Design of Experiments (Full Factorial) Efficiency Gain
Total Experiments Required 15 (3 factors * 3 levels + center point repeats) 27 (3³) or 15 (with fractional design) DoE can be more efficient with smart design
Ability to Detect Interactions No Yes Critical for complex systems [4]
Modeling Capability Linear, single-factor only Full quadratic response surface Enables optimization and prediction
Resource Utilization Inefficient; high runs per unit information Efficient; maximizes information per run DoE conserves time, materials, and cost [4]

The DoE Workflow: A Step-by-Step Technical Guide

Phase 1: Planning and Experimental Design

The first phase transforms a research question into an executable experimental matrix.

  • Define Objective and Responses: Clearly state the goal (e.g., maximize yield, purity, or device efficiency) and identify measurable responses (e.g., External Quantum Efficiency (EQE), conversion %) [13].
  • Select Factors and Levels: Choose input variables (e.g., catalyst loading (M), temperature (T), solvent ratio (S)) and their high/low/center levels based on prior knowledge or screening [13] [4]. This step is critical for bounding the experimental space.
  • Choose an Experimental Design: The design selection depends on the goal:
    • Screening: Use Plackett-Burman (PBD) or definitive screening designs to identify the most influential factors from a large set with minimal runs [4].
    • Optimization: Use Response Surface Methodology (RSM) designs like Central Composite Design (CCD) or Box-Behnken Design (BBD) to model curvature and locate optima [44]. For systems with categorical factors (e.g., catalyst type), Taguchi designs can be effective [44].
    • Mixture Design: Used when factors are components of a mixture that sum to 100% [45].

The following diagram outlines the high-level decision logic for selecting a DoE design within a broader research program.

G Start Research Objective Screening Initial Factor Screening? Start->Screening ManyFactors Many Potential Factors? Screening->ManyFactors Yes ModelOpt Model & Optimize Response Surface? Screening->ModelOpt No PBD Use Plackett-Burman (PBD) or Definitive Screening Design ManyFactors->PBD Yes ManyFactors->ModelOpt No CatFactor Categorical Factors Present? ModelOpt->CatFactor Yes Mixture Mixture/Formulation Problem? ModelOpt->Mixture No CCD Use Central Composite Design (CCD) or Box-Behnken CatFactor->CCD No Taguchi Use Taguchi Design for Categorical Levels CatFactor->Taguchi Yes Mixture->PBD No (General Screening) MixDesign Use Mixture Design Mixture->MixDesign Yes

Diagram 1: DoE Design Selection Logic (86 chars)

Phase 2: Randomization and Execution

To mitigate the effects of lurking variables (e.g., ambient temperature, reagent batch variations), the run order prescribed by the design matrix must be randomized [4]. This is a non-negotiable step to ensure that noise is distributed independently across all factor combinations, validating the statistical analysis. The actual experiments are then conducted strictly according to the randomized run sheet.

Phase 3: Data Collection and Analysis

Data is collected for each response variable. Statistical analysis (typically Analysis of Variance - ANOVA) is performed to assess the significance of main effects and interactions. The results are often modeled via regression to create a predictive equation. Machine learning techniques (e.g., Support Vector Regression (SVR)) can further augment this analysis, especially for highly complex or non-linear response surfaces [13] [46].

Case Study 1: Optimizing OLED Device Performance via DoE+ML

Experimental Protocol (Adapted from Ikemoto et al., 2025) [13]:

  • Objective: Optimize a macrocyclization reaction to produce a crude mixture for direct use in OLEDs, eliminating purification.
  • Factors & Levels: 5 factors at 3 levels: Ni(cod)â‚‚ equivalent (M: 1.5, 2.0, 2.5), addition time (T: 1, 5, 9 hr), concentration (C: 20, 50, 80 mM), reactant ratio R (5, 50, 95%), solvent composition S (5, 50, 95% DMF).
  • Design: An L18 Taguchi orthogonal array (accommodating 5 factors at 3 levels in 18 runs) [13].
  • Response: External Quantum Efficiency (EQE) of the fabricated OLED device.
  • Workflow: 18 reactions were performed per design → Crude mixtures were spin-coated with an Ir emitter to form emission layers → Devices were completed and EQE measured in quadruplicate.
  • Analysis & ML Integration: EQE data was used to train ML models (SVR, PLSR, MLP). SVR showed the best predictive performance via leave-one-out cross-validation (MSE=0.0368) and was used to generate a predictive heatmap of the 5D parameter space [13].
  • Validation: The model-predicted optimal condition (M=2, T=9, C=64, R=5, S=33) yielded an experimental EQE of 9.6%, surpassing the performance of devices made with purified materials (~0.9%) [13].

Table 2: Key Results from OLED Optimization DoE Study [13]

Metric DoE+ML Optimal (Crude Mixture) Purified [5]CMP Material Efficiency Gain
External Quantum Efficiency (EQE) 9.6 ± 0.1% 0.9 ± 0.1% > 10x improvement
Process Steps to Device Reaction → Work-up → Device Fabrication Reaction → Purification → Device Fabrication Eliminated energy/waste of purification
Optimal Condition M=2, T=9hr, C=64mM, R=5%, S=33% Not applicable Identified via systematic exploration

The integrated DoE and machine learning workflow for this study is visualized below.

G cluster_doe DoE Phase cluster_ml ML Phase cluster_ver Verification A Define 5 Factors & 3 Levels (M, T, C, R, S) B Select Taguchi L18 Orthogonal Array A->B C Perform 18 Randomized Reactions & Fabricate OLEDs B->C D Measure Device Response (EQE x 4 replicates) C->D E Train Predictive Models (SVR, PLSR, MLP) D->E Dataset F Validate & Select Best Model (LOOCV → SVR) E->F G Generate Predictive Heatmap of 5D Space F->G H Identify Global EQE Maximum G->H I Run Validation Experiment at Predicted Optimum H->I Optimal Conditions J Achieve High EQE (9.6%) with Crude Mixture I->J

Diagram 2: DoE+ML Workflow for OLED Optimization (72 chars)

Case Study 2: Screening Key Factors in Cross-Coupling Reactions

Experimental Protocol (Adapted from Scientific Reports, 2025) [4]:

  • Objective: Screen and rank the importance of five key factors in three classic C–C cross-coupling reactions.
  • Factors & Levels: 5 factors at 2 levels: Ligand electronic effect (vCO), Ligand cone angle (θ), Catalyst loading (1 vs 5 mol%), Base (Et₃N vs NaOH), Solvent polarity (DMSO vs MeCN).
  • Design: A 12-run Plackett-Burman (PBD) screening design. This saturated design efficiently estimates main effects using all degrees of freedom [4].
  • Response: Conversion or yield for Mizoroki–Heck, Suzuki–Miyaura, and Sonogashira–Hagihara reactions.
  • Workflow: Reactions were set up in carousel tubes according to the randomized PBD matrix and run at 60°C for 24 hours. Conversions were analyzed by GC or similar methods.
  • Analysis: Statistical analysis of the PBD data identified which factors (e.g., ligand properties, base strength) had significant main effects on each reaction type, providing a data-driven guide for subsequent, more detailed optimization using RSM [4].

The Scientist's Toolkit: Essential Research Reagent Solutions

Table 3: Key Reagents & Materials for DoE in Organic/Materials Synthesis

Item Function & Relevance to DoE Example from Case Studies
Taguchi Orthogonal Arrays Pre-defined statistical matrices that allow efficient study of multiple factors with minimal runs, ideal for initial optimization. L18 array used to study 5 factors at 3 levels in OLED study [13].
Plackett-Burman (PBD) Designs Saturated screening designs for identifying the most influential factors from a large set; foundational for efficient factor selection. 12-run PBD used to screen 5 factors in cross-coupling reactions [4].
Central Composite Design (CCD) A gold-standard RSM design for building a second-order (quadratic) model, enabling location of optima and response surface mapping. Recommended for final optimization after screening, especially with continuous factors [44].
Machine Learning Libraries (e.g., for SVR, MLP) Tools for modeling complex, non-linear relationships between factors and responses, extending the predictive power of DoE data. SVR model used to predict OLED performance across a 5D parameter space [13].
High-Throughput Experimentation (HTE) Equipment Carousel reactors, automated liquid handlers. Enables the practical execution of the numerous, randomized experiments required by DoE. Reactions performed in carousel tubes to efficiently execute the PBD [4].
Statistical Analysis Software Software (e.g., JMP, Stat-Ease 360, R, Python) for design generation, randomization, and analysis of variance (ANOVA). Essential for deriving actionable insights from experimental data [45].
19-Methyltetracosanoyl-CoA19-Methyltetracosanoyl-CoA, MF:C46H84N7O17P3S, MW:1132.2 g/molChemical Reagent
6-Methylpentadecanoyl-CoA6-Methylpentadecanoyl-CoA, MF:C37H66N7O17P3S, MW:1005.9 g/molChemical Reagent

The presented workflow—from strategic design selection and rigorous randomization to data collection enhanced by ML—demonstrates a superior pathway for knowledge generation compared to OFAT. The case studies underscore that DoE is not merely a statistical tool but a comprehensive framework for efficient resource allocation and deep process understanding [13] [4]. While DoE has limitations, including complexity and reliance on model assumptions [47], its capacity to efficiently manage multi-factor interactions makes it indispensable for modern organic synthesis and drug development. Embracing this workflow allows researchers to systematically navigate complex chemical spaces, accelerate optimization, and deliver innovative solutions with greater speed and confidence.

In the field of organic synthesis, the optimization of reaction conditions is a critical, yet often resource-intensive, step. Traditionally, this has been dominated by the One-Factor-At-a-Time (OFAT) approach, where a single variable is altered while all others are held constant [48] [13]. While intuitive and useful for simple reactions with straightforward pathways, OFAT optimization carries significant limitations for complex processes, especially those involving multiple performance metrics. It inefficiently explores the experimental space, fails to capture interaction effects between variables, and can miss the true optimum conditions, often resulting in a suboptimal compromise between responses like yield and selectivity [10].

In contrast, Design of Experiments (DoE) is a statistical methodology that systematically varies multiple factors simultaneously. This approach, a mainstay in industrial process chemistry, provides a robust model for understanding how factors individually and interactively influence the response(s) of interest [49] [10]. The core advantage of DoE is its ability to map a multidimensional experimental space with a minimized number of experiments, revealing optimal conditions that OFAT might never discover [10]. This case study details a groundbreaking application of DoE, combined with machine learning (ML), to directly optimize the performance of an organic light-emitting device (OLED) by tuning the conditions of the macrocyclization reaction that produces its core material, thereby bridging synthetic chemistry and device engineering [48] [13].

This case study is based on a 2024 study that developed a "from-flask-to-device" optimisation strategy for a macrocyclisation reaction yielding a mixture of methylated [n]cyclo-meta-phenylenes ([n]CMPs), which served as host materials in Ir-doped OLEDs [48] [13]. The innovation lay in directly applying the crude raw material from the reaction to device fabrication via spin-coating, intentionally bypassing energy-consuming and waste-producing separation and purification steps [48]. This approach aligns with green chemistry principles, reducing solvent and reagent usage and minimizing chemical waste [49] [10].

The primary goal was to use the DoE + ML method to correlate the macrocyclisation reaction conditions directly with the final OLED performance, measured by External Quantum Efficiency (EQE), rather than with an intermediate metric like isolated yield [48]. Remarkably, the optimal raw mixture achieved a high EQE of 9.6%, surpassing the performance of devices fabricated with purified materials (EQE = 0.9%) [48] [13]. This demonstrated that a meticulously designed mixture of congeners could outperform a pure single compound, a formulation that would be exceedingly difficult to achieve through traditional separation and purification [48].

Experimental Design and Workflow

Defining the Optimization Problem

The system involved a Yamamoto-type macrocyclisation of dihalotoluene (1) to produce a mixture of methylated [n]CMP congeners (n ≥ 5) [48] [13]. The objective was not to maximize the yield of a single [n]CMP, but to find the reaction conditions that produced a mixture which, when used as a host material in an OLED, resulted in the highest device EQE.

Selected Factors and Levels

Five key reaction factors, previously identified as influential, were selected for optimization. Each factor was examined at three levels [48] [13].

Table 1: Factors and Levels for the DoE Optimization

Factor Code Factor Description Level 1 Level 2 Level 3
M Equivalent of Ni(cod)â‚‚ 1.5 2.0 2.5
T Dropwise addition time of 1 (h) 1 9 17
C Final concentration of 1 (mM) 10 50 90
R % content of bromochlorotoluene (1b) in 1 5 50 95
S % content of DMF in solvent 5 50 95

The DoE + ML Workflow

The experimental workflow seamlessly integrated DoE with machine learning prediction and validation.

workflow Start Define Objective: Correlate Reaction Conditions with OLED EQE A Select Factors & Levels (M, T, C, R, S) Start->A B Choose DoE Design: Taguchi L18 Orthogonal Array A->B C Execute 18 Reactions Prepare Crude Mixtures B->C D Fabricate OLED Devices Measure EQE Response C->D E Machine Learning: Train SVR Model on Data D->E F Grid Search & Prediction Identify Optimal Conditions E->F G Experimental Validation Test Run at Predicted Optimum F->G End Optimal Conditions Found EQE = 9.6% G->End

Figure 1: The integrated DoE and machine learning workflow for optimizing OLED performance.

Step 1: Experimental Design and Execution

An L18 (2¹ × 3⁷) Taguchi orthogonal array was selected, which required only 18 experimental runs to model the 5-factor, 3-level space [48] [13]. The 18 reactions were performed under the designed conditions, and the crude products were worked up with a short silica gel column to remove only metal and polar residues [48].

Step 2: Device Fabrication and Response Measurement

Each of the 18 crude raw materials was used to fabricate a double-layer OLED [48]. The device structure was:

  • Emission Layer (EML): Spin-coated from a solution of the crude [n]CMP mixture and an Ir emitter (3) (14 wt% in the layer), thickness = 20 nm.
  • Electron Transport Layer (ETL): Sublimated 1,3,5-tris(1-phenyl-1H-benzimidazol-2-yl)benzene (TPBi, 2), thickness = 60 nm [48] [13]. The device performance for each set of conditions was evaluated by measuring the EQE in quadruplicate [48].
Step 3: Machine Learning and Prediction

The dataset of five reaction factors (M, T, C, R, S) and the corresponding EQE response was used to train machine learning models [48]. Three methods were evaluated:

  • Support Vector Regression (SVR)
  • Partial Least Squares Regression (PLSR)
  • Multilayer Perceptron (MLP) The models were compared using Leave-One-Out Cross-Validation (LOOCV), and the SVR model demonstrated the lowest Mean Square Error (MSE = 0.0368) and was selected as the final predictor [48] [13]. The SVR model generated a predictive heatmap across the five-dimensional parameter space.
Step 4: Validation and Discovery

A grid search of the SVR model predicted the highest EQE (11.3%) at conditions (M, T, C, R, S) = (2, 9, 64, 5, 33) [48] [13]. An experimental test run at these conditions yielded a device with an EQE of 9.6% ± 0.1%, successfully validating the model. A second test run at another predicted high-performance point also showed good agreement, confirming the model's credibility [48].

Key Reagents and Materials

The following table details the key reagents and materials essential for replicating this optimized process.

Table 2: Key Research Reagent Solutions and Materials

Reagent/Material Function / Role in the Experiment Specification / Notes
Dihalotoluene (1) Starting monomer for macrocyclization A mixture of dibromo- and bromochlorotoluene; ratio is a key factor (R) [48].
Ni(cod)â‚‚ Main catalyst for Yamamoto coupling Equivalent used is a key factor (M) [48].
DMG Ligand for Ni-catalyst -
DMF / Toluene Solvent system Ratio is a key factor (S) [48].
Ir Emitter (3) Phosphorescent dopant in OLED -
TPBi (2) Electron Transport Layer (ETL) material Sublimated to form a 60 nm layer [48] [13].
ITO-coated Glass OLED anode substrate -

Results and Analysis

DoE vs. OFAT: A Conceptual Comparison

The fundamental difference between the DoE approach and the traditional OFAT method is visually and conceptually stark.

comparison cluster_OFAT OFAT Approach cluster_DoE DoE + ML Approach A Vary Factor M Hold T, C, R, S constant B Find 'Best' M A->B C Vary Factor T Hold M, C, R, S at 'Best' B->C D Find Compromised Optimum C->D E Systematically Vary M, T, C, R, S Together F Measure OLED EQE for All Combinations E->F G ML Model Maps Entire Parameter Space F->G H Discover True Global Optimum G->H

Figure 2: A conceptual comparison of the OFAT and DoE methodologies, highlighting the systematic and comprehensive nature of DoE.

Performance Comparison: Raw Mixture vs. Pure Materials

A critical finding of this study was the superior performance of the optimized raw mixture over purified single compounds.

Table 3: Performance Comparison of OLED Devices

Host Material Type Specific Conditions / Compound External Quantum Efficiency (EQE) Key Finding
Optimized Raw Mixture DoE Optimum: (M, T, C, R, S) = (2, 9, 64, 5, 33) 9.6% ± 0.1% Surpasses purified materials; mixture prevents crystallization [48] [13].
Purified Single Congeners Methylated [5]CMP 0.9% ± 0.1% Performance is inferior due to crystalline character from spin-coating [48].
Purified Single Congeners Methylated [6]CMP 0.8% ± 0.3% Performance is inferior due to crystalline character from spin-coating [48].

The MALDI-TOF mass spectrometry analysis of the optimal raw material revealed a complex mixture of congeners ([5]CMP to [15]CMP), with the majority population being [5]CMP (19%), [6]CMP (26%), and [7]CMP (18%) [48]. This specific distribution, which is responsible for maintaining an amorphous film state and high device performance, is a direct result of the optimized reaction conditions and would be practically impossible to formulate through traditional means [48].

This case study successfully demonstrates a powerful "from-flask-to-device" optimisation paradigm using a combined DoE and ML strategy. By systematically correlating synthetic chemistry parameters with final device performance, the research achieved two major outcomes:

  • It identified a set of macrocyclization reaction conditions that produced a crude mixture capable of yielding high-performance OLEDs, eliminating the need for costly purification.
  • It revealed that a complex molecular mixture can outperform highly purified single compounds in optoelectronic device applications, challenging conventional material selection wisdom.

The demonstrated methodology provides a robust framework for accelerating the development of functional organic materials while adhering to the principles of green chemistry. This approach is particularly valuable for optimizing multistep processes where the final performance metric is difficult to predict from intermediate characteristics alone. The significant performance and efficiency advantages of DoE over OFAT, as detailed in this case study, make a compelling argument for its wider adoption in academic and industrial synthetic research [48] [13] [10].

In organic synthesis and drug development, the One-Factor-At-a-Time (OFAT) approach has long been the traditional method for reaction optimization. This method involves systematically changing a single variable while keeping all others constant, which is particularly useful for reactions with simple pathways and can provide mechanistic insights [13]. However, OFAT optimization presents significant limitations for complex systems with interacting factors, as it inefficiently explores the experimental parameter space and often fails to identify optimal conditions when multiple variables influence outcomes simultaneously [13].

Design of Experiments (DoE) represents a fundamental shift in experimental strategy, enabling researchers to efficiently explore multiple factors and their interactions through structured experimental designs. For reactions with complicated pathways, DoE optimization often proves superior because it more effectively covers the parameter space for optimization [13]. The pharmaceutical and organic synthesis communities are increasingly recognizing DoE's value, with recent advancements combining DoE with machine learning (ML) strategies to correlate reaction conditions with performance outcomes in multistep fabrication processes [13].

Despite its advantages, DoE adoption has faced barriers related to methodological complexity and the statistical knowledge required for implementation. This technical guide explores how modern software tools are dismantling these barriers, making DoE methodologies accessible to researchers across experience levels while maintaining statistical rigor.

The Software Landscape: DoE Tools for Modern Research

The current DoE software market offers solutions ranging from specialized tools for specific scientific domains to comprehensive statistical platforms. These tools are specifically designed to help researchers understand cause and effect using the power of statistically designed experiments, even when working with limited resources [50].

Table 1: Comparison of DoE Software Platforms

Software Platform Primary Focus Key Features Target Audience
Synthace DOE Life Sciences Biology Curated designs for life sciences, automated experiment instructions, in-silico design validation, automatic data structuring Biologists, Life Science Researchers
JMP General Statistical Analysis Custom Designer for real-world constraints, Definitive Screening Designs for many factors, comprehensive visualization Industrial Scientists, Statisticians
Design-Expert Product/Process Optimization Interactive 2D graphs and 3D plots, simultaneous multi-response optimization, combined study types Process Engineers, Formulation Scientists
Stat-Ease 360 Advanced DOE Integration Python integration, computer experiments, advanced analysis capabilities Advanced DOE Practitioners, Data Scientists

Lowering the Barrier to Entry

Modern DoE platforms specifically address historical adoption barriers through several key innovations:

  • Simplified Design Selection: Platforms like Synthace offer "a curated list of designs for life sciences that adapt as you iterate if the intent or context changes," eliminating the complexity of choosing appropriate experimental designs [51].
  • Visual Analysis Interfaces: Tools such as Design-Expert provide "interactive 2D graphs" and "rotatable 3D plots" that make complex statistical concepts visually accessible [52].
  • Automated Implementation Guidance: Software generates "accurate automation instructions from your design, automatically," reducing translation errors between experimental design and laboratory execution [51].
  • Accessible Analysis Tools: Platforms enable users to "build models directly from results and get a summary analysis of the preferred model without statistics skills," democratizing advanced analytical capabilities [51].

These innovations collectively address the "high turn-over of researchers in academic settings [that] presents an additional challenge to training students on how to strategically implement HTE [High-Throughput Experimentation] in their research endeavors" [14].

DoE in Action: Case Study in Organic Electronics

Experimental Background and Objectives

A recent study exemplifies the powerful integration of DoE with machine learning in organic synthesis. Researchers aimed to optimize reaction conditions for macrocyclization reactions yielding methylated [n]cyclo-meta-phenylenes ([n]CMPs), which serve as materials for Ir-doped organic light-emitting devices (OLEDs) [13].

The research objective was to correlate reaction conditions directly with device performance, enabling "from-flask-to-device" optimisation that eliminated energy-consuming and waste-producing separation and purification steps during device fabrication [13]. This approach aligned with important principles of green and sustainable chemistry while maintaining high device performance.

DoE Experimental Design and Protocol

Experimental Design Factors and Levels: The researchers selected five factors previously identified as influential in Yamamoto macrocyclization: equivalent of Ni(cod)â‚‚ (M), dropwise addition time of dihalotoluene 1 (T), final concentration of 1 (C), percentage content of bromochlorotoluene (1b) in 1 (R), and percentage content of DMF in solvent (S) [13]. Each factor was examined at three levels, resulting in 5 factors and 3 levels for optimization.

Taguchi Orthogonal Array Implementation: The experimental parameter space was set using the "L18 (2¹ × 3⁷)" table from Taguchi's orthogonal arrays, with 5×18 cells selected to cover the 5 factors [13]. This efficient experimental design enabled comprehensive exploration of the parameter space with only 18 experimental runs instead of the 3⁵=243 runs required for a full factorial approach.

Device Fabrication and Evaluation: For each of the 18 reactions conducted under the designed conditions, crude raw materials were obtained after aqueous workup and passing through a short-path silica gel column to remove metal and polar residues [13]. Double-layer OLEDs were fabricated by spin-coating a solution of the crude raw mixture of methylated [n]CMPs mixed with an Ir emitter (14 wt% in the layer) as the emission layer (20 nm), then sublimating 1,3,5-tris(1-phenyl-1H-benzimidazol-2-yl)benzene (TPBi) as the electron transport layer (60 nm) [13]. Device performance was evaluated by external quantum efficiency (EQE) in quadruplicate to correlate the five reaction factors with EQE performance.

Machine Learning Integration: The DoE optimization data was augmented with machine learning predictions using three methods: support vector regression (SVR), partial least squares regression (PLSR), and multilayer perceptron (MLP) to obtain EQE heatmaps filling the five-dimensional parameter space [13]. The SVR model was selected as the most appropriate predictor based on mean square errors obtained via leave-one-out cross-validations, then validated through test runs that confirmed the model's credibility [13].

DOE_Workflow Start Define Research Objective:    Optimize OLED Performance FactorSelection Select Factors and Levels:    M, T, C, R, S (3 levels each) Start->FactorSelection DoEDesign Apply Taguchi Orthogonal Array:    L18 (2¹ × 3⁷) Design FactorSelection->DoEDesign Experimentation Execute 18 Reactions    Under Designed Conditions DoEDesign->Experimentation DeviceFabrication Fabricate OLED Devices    Using Crude Reaction Mixtures Experimentation->DeviceFabrication PerformanceEval Evaluate Device Performance:    Measure External Quantum Efficiency (EQE) DeviceFabrication->PerformanceEval MLIntegration Apply Machine Learning:    SVR, PLSR, MLP Models PerformanceEval->MLIntegration ModelValidation Validate Predictive Model    Through Test Runs MLIntegration->ModelValidation Optimization Identify Optimal Conditions    For Maximum EQE ModelValidation->Optimization

Figure 1: Integrated DoE and ML Workflow for OLED Material Optimization

Research Reagent Solutions and Materials

Table 2: Key Research Materials and Reagents

Material/Reagent Function in Experiment Significance
Dihalotoluene (1) Starting material for Yamamoto macrocyclization Precursor for methylated [n]CMP synthesis
Ni(cod)â‚‚ Catalyst for Yamamoto coupling Mediates macrocyclization reaction
Bromochlorotoluene (1b) Reactant component Modifies product distribution via kinetics
DMF Solvent component Influences disproportionation step kinetics
Ir emitter (3) Dopant for OLED devices Provides electroluminescent centers
TPBi (2) Electron transport layer material Facilitates electron injection/transport

Results and Validation

The DoE+ML approach successfully identified optimal reaction conditions that maximized OLED performance. The grid search of the five-dimensional SVR model identified the highest predicted EQE spot of 11.3% at specific factor combinations, and actual test runs at this condition yielded a comparable EQE value of 9.6±0.1% [13]. This performance surpassed devices fabricated using purified materials, which recorded significantly lower EQE values of 0.9±0.1% and 0.8±0.3% for methylated [5]CMP and [6]CMP respectively [13].

Analysis of the optimal raw material revealed a mixture of methylated [n]CMP congeners (n=5-15) with specific population distributions, suggesting that the mixture's amorphous character better maintained host material performance through the solution process of spin coating compared to pure materials that exhibited problematic crystalline character [13].

OFAT_vs_DOE OFAT OFAT Approach OFAT1 Change Single Factor    Hold Others Constant OFAT->OFAT1 OFAT2 Linear Progression    Through Parameter Space OFAT1->OFAT2 OFAT3 Misses Interactions    Between Factors OFAT2->OFAT3 OFAT4 Inefficient Use of    Experimental Resources OFAT3->OFAT4 DOE DoE Approach DOE1 Vary Multiple Factors    Simultaneously DOE->DOE1 DOE2 Structured Exploration    Of Parameter Space DOE1->DOE2 DOE3 Identifies Factor    Interactions DOE2->DOE3 DOE4 Efficient Resource Use    With Fewer Experiments DOE3->DOE4

Figure 2: Comparative Methodology: OFAT vs. DoE Experimental Strategies

Implementation Guidelines: Integrating DoE Software into Research Workflows

Strategic Software Selection

Choosing appropriate DoE software requires careful consideration of research objectives, team expertise, and integration needs:

  • Domain Specialization: Biologists and life scientists may benefit from platforms like Synthace that offer "curated designs for life sciences," while engineers might prefer Design-Expert's focus on "product and process optimization" [51] [52].
  • Analysis Capabilities: Teams without dedicated statisticians should prioritize tools that provide "summary analysis of the preferred model without statistics skills" [51].
  • Iterative Flexibility: Research environments requiring frequent protocol adjustments need software where "designs adapt as you iterate if the intent or context changes" [51].
  • Integration Potential: Advanced teams should consider platforms like Stat-Ease 360 that enable "Python integration" for custom analytical workflows [52].

Best Practices for Successful Implementation

Successful DoE implementation extends beyond software selection to encompass methodological considerations:

  • Factor Prioritization: As demonstrated in the OLED case study, selecting factors based on mechanistic understanding and preliminary data ensures efficient experimental designs [13].
  • Appropriate Scaling: While HTE approaches enable "testing 1536 reactions simultaneously," researchers should balance throughput with analytical capabilities and resource constraints [14].
  • Bias Mitigation: Especially in miniaturized formats, address potential "spatial bias due to discrepancies between center and edge wells" through randomized run orders and technical replicates [14].
  • Data Management: Adhere to FAIR principles (Findable, Accessible, Interoperable, and Reusable) to maximize the long-term value of DoE-generated data [14].

Industry reports quantify the impact of these approaches, with organizations reporting "savings of at least 50% of the time and resources" through DoE implementation, reaching "even 70%" in some cases [50].

The integration of sophisticated software tools with DoE methodologies is fundamentally transforming research approaches in organic synthesis and drug development. By lowering the historical barriers to entry—statistical complexity, design selection challenges, and analytical interpretation—modern platforms are democratizing access to efficient experimental strategies that extract maximum information from limited resources.

The case study in organic electronics demonstrates the powerful synergy between structured experimental designs and machine learning, enabling researchers to navigate complex multi-parameter spaces and achieve performance outcomes inaccessible through traditional OFAT approaches. As these tools continue evolving toward "fully integrated, flexible, and democratized platforms," they promise to accelerate innovation across chemical and pharmaceutical research [14].

The transition from OFAT to DoE represents more than a methodological shift—it embodies a fundamental evolution in scientific thinking toward systems-based, multidimensional experimentation. Software tools that continue to lower implementation barriers while maintaining statistical rigor will play a pivotal role in this paradigm shift, empowering researchers to tackle increasingly complex scientific challenges with greater efficiency and insight.

Overcoming Common Pitfalls and Advanced Optimization Strategies

Why OFAT Fails to Identify Critical Factor Interactions

In the realm of organic synthesis research, the optimization of chemical reactions is a cornerstone of developing efficient, sustainable, and scalable methodologies. For decades, the One-Factor-at-a-Time (OFAT) approach has been a default strategy, favored for its intuitive and straightforward implementation [2] [1]. This method involves systematically varying a single experimental parameter—such as temperature, catalyst loading, or solvent—while holding all others constant. However, within the context of a broader thesis advocating for the supremacy of Design of Experiments (DoE), it becomes critically evident that OFAT possesses a fundamental and crippling flaw: its inherent inability to detect and quantify interactions between factors [2] [9]. This whitepaper delves into the technical reasons for this failure, substantiated by quantitative data and case studies, ultimately framing DoE as the statistically rigorous and information-rich alternative essential for modern research and drug development.

The Core Limitation: A Blind Spot to Interactions

The primary failure of OFAT stems from its foundational premise. By altering only one variable per experimental series, it operates under the implicit assumption that all factors act independently on the response (e.g., reaction yield, selectivity). In complex chemical systems, this is rarely true. Factors often interact, meaning the effect of one variable (e.g., temperature) depends significantly on the level of another (e.g., catalyst concentration) [2] [53].

  • Statistical Blindness: OFAT experiments are not designed to estimate interaction effects. The data structure generated—a series of univariate datasets—lacks the necessary combinatorial framework for interaction analysis provided by factorial designs [54].
  • Misleading Optima: As graphically demonstrated in a seminal example, an OFAT optimization can easily converge on a local optimum, completely missing the true global optimum that exists due to factor interactions [9]. An initial OFAT search might optimize Factor A while holding Factor B fixed, then optimize Factor B using the new level of A. This path-dependent search can bypass superior combinations of A and B that were never tested [9].
  • Inefficiency and Resource Waste: To naively explore interactions via OFAT would require an impractical number of experiments. For k factors, a full exploration of just two levels each would require a minimum of 2^k runs in a factorial design, but a vastly larger and less systematic number in an OFAT framework to achieve the same insight [2].

The following table summarizes the comparative inability of OFAT to manage experimental complexity:

Table 1: Core Capabilities Comparison: OFAT vs. Factorial DoE

Capability OFAT Approach Factorial DoE Implication for Synthesis Research
Detects Main Effects Yes, but with lower precision [1]. Yes, with higher precision and statistical confidence [2]. DoE gives more reliable estimates of individual factor importance.
Detects Factor Interactions No. It is fundamentally incapable [2] [1]. Yes. Designed specifically to quantify 2-way, 3-way, etc., interactions [53] [54]. Critical for understanding synergistic/antagonistic effects between e.g., catalyst and ligand.
Experimental Efficiency Low. Requires many runs for equivalent precision; runs grow linearly with factors but information gain is limited [2]. High. Maximizes information per run; effect estimates are based on all data [2] [49]. Saves time, material, and cost, aligning with Green Chemistry principles [49].
Optimization Power Weak. Prone to finding sub-optimal local maxima/minima [9]. Strong. Enables mapping of response surfaces and navigation to global optima [39]. Crucial for achieving the highest yield, selectivity, or process robustness.
Error Estimation Poor. Requires explicit replication to estimate noise [2]. Built-in. Replication and randomization provide clear estimate of experimental error [2] [55]. Allows researchers to distinguish real effects from background noise.

Case Studies in Failure and Success

The Hypothetical Interaction Trap

A classic tutorial example illustrates the peril. Imagine optimizing a reaction for yield by varying reagent equivalents (Factor A) and temperature (Factor B) via OFAT [9]. Holding temperature at 40°C, varying equivalents suggests 2.0 eq is optimal. Fixing equivalents at 2.0, varying temperature suggests 55°C is optimal. The OFAT conclusion is (2.0 eq, 55°C). However, a full factorial DoE reveals a strong interaction: at very high temperatures (e.g., 105°C), much lower reagent loading (1.25 eq) yields a significantly superior outcome—a condition never examined in the OFAT sequence [9].

Organic Light-Emitting Device (OLED) Material Synthesis

A modern research application underscores the point. Optimizing a macrocyclization reaction for OLED performance involved five factors (e.g., catalyst equivalent, addition time, concentration). An OFAT approach would be overwhelmingly complex. Researchers employed a DoE (Taguchi L18 array) coupled with machine learning to model the five-dimensional parameter space [13]. This DoE+ML strategy successfully correlated reaction conditions directly with final device efficiency (External Quantum Efficiency, EQE), identifying an optimal mixture that outperformed purified materials—a result unimaginable through sequential OFAT testing [13].

Table 2: Quantitative Outcomes from DoE-led Optimization Studies

Study / Reaction Factors OFAT Implication DoE Approach & Outcome Key Interaction Discovered
General Case [9] 2 (Equivalents, Temp) Would find sub-optimal local optimum. Full factorial revealed true global optimum. Significant interaction between equivalents and temperature.
OLED Macrocyclization [13] 5 (M, T, C, R, S) Prohibitively long, likely misses optimal mixture. L18 Orthogonal Array + SVR ML model. Achieved EQE of 9.6%. Complex multi-factor interactions modeled to optimize product distribution for device performance.
Wacker Oxidation [49] 7 (Substrate, Cat., Temp., Time, etc.) Inefficient, hard to rank factor importance. Screening DoE identified catalyst amount, temperature, and co-catalyst as critical with interactions affecting selectivity. Interactions between catalyst amount and reaction temperature pivotal for directing anti-Markovnikov selectivity to aldehyde.
Solvent Optimization [9] Solvent Properties (via PCA) Trial-and-error based on intuition. DoE across a "solvent space map" identifies optimal solvent region based on properties. Interaction between solvent polarity and donor number affecting reaction pathway.

Detailed Experimental Protocol: Implementing a DoE to Uncover Interactions

The following protocol, synthesized from cited studies [13] [49], provides a framework for replacing OFAT with a screening factorial design.

Objective: To identify the main effects and two-factor interactions critical for the yield of a catalytic transformation.

Step 1: Define Factors and Levels.

  • Select 3-4 continuous or categorical factors suspected to influence the reaction (e.g., Catalyst Loading (mol%), Temperature (°C), Reaction Time (h), Solvent Type).
  • For continuous factors, define a high (+1) and low (-1) level representing a reasonable experimental range.
  • For a categorical factor like solvent, assign two representative solvents to the +1 and -1 levels.

Step 2: Choose Experimental Design.

  • For 3 factors, use a full 2^3 factorial design (8 experiments).
  • Include 3-5 center point replicates (all factors at midpoint) to estimate pure error and check for curvature.
  • Randomize the run order of all 11-13 experiments to mitigate confounding from lurking variables.

Step 3: Execution and Data Collection.

  • Prepare reagents and set up reactions according to the randomized worksheet.
  • Conduct all reactions under controlled conditions, using standardized work-up and analysis protocols (e.g., HPLC, NMR) to determine yield or conversion.
  • Record responses meticulously.

Step 4: Statistical Analysis.

  • Input data into statistical software (JMP, Minitab, R).
  • Perform Analysis of Variance (ANOVA) on the factorial model including main effects and interaction terms.
  • Evaluate p-values (typically <0.05) to identify statistically significant effects.
  • Examine interaction plots: Non-parallel lines indicate the presence of an interaction. For example, if the plot of Yield vs. Temperature for two different catalyst loadings shows crossing or diverging lines, a significant Temperature*Catalyst interaction exists [53] [54].

Step 5: Interpretation and Path Forward.

  • The analysis will rank factors by significance and reveal which interactions are important.
  • If curvature (suggested by center points) is significant, proceed to a Response Surface Methodology design (e.g., Central Composite Design) for optimization [39] [55].
  • Verify the model by running a confirmation experiment at the predicted optimal conditions.

Visualization of Experimental Philosophies

OFAT_Workflow OFAT Sequential Linear Process cluster_interaction Interaction Space Not Explored Start Start: Baseline Conditions (A0,B0) FixB Fix Factor B at B0 Vary Factor A Start->FixB OptA Determine Optimal A* FixB->OptA Missed Potential True Optimum (A', B') FixA Fix Factor A at A* Vary Factor B OptA->FixA OptB Determine Optimal B* FixA->OptB OFAT_End OFAT Conclusion: Optimum at (A*, B*) OptB->OFAT_End

DOE_Workflow DoE Parallel Factorial Design Start Define Factors & Levels (A, B) Design Create 2^2 Factorial Design 4 Runs: (A-,B-), (A+,B-), (A-,B+), (A+,B+) Start->Design Parallel Execute All Runs in Random Order Design->Parallel Analyze Statistical Analysis: - Main Effects - A*B Interaction Parallel->Analyze Model Build Predictive Model Identify True Optimum Analyze->Model IntNode Interaction Effect Quantified & Visualized Analyze->IntNode

The Scientist's Toolkit: Essential Reagents & Solutions for DoE-led Synthesis

Table 3: Key Research Reagent Solutions for Interaction-Focused Optimization

Reagent / Material Category Specific Example(s) Primary Function in DoE Context
Catalyst Systems PdCl2(MeCN)2, Ni(cod)2, Organocatalysts [13] [49] The primary factor to optimize; often involved in strong interactions with ligands, solvents, and temperature.
Co-catalysts / Oxidants CuCl2, Benzoquinone, Molecular Oxygen [49] Secondary factors whose optimal loading is frequently dependent on (interacts with) catalyst loading and reaction conditions.
Solvent Libraries Diverse set spanning polarity, donor number, dielectric constant [9] A categorical or continuous factor (via solvent properties) with profound interactions, especially in transition metal catalysis.
Orthogonal Array Kits Pre-defined matrices (e.g., Taguchi L18) [13] Provides a ready-made experimental layout for screening multiple factors at multiple levels with minimal runs.
Statistical Software JMP, Minitab, R with DoE packages [56] [55] Essential for generating randomized designs, analyzing ANOVA results, plotting interactions, and building response surface models.
Parallel Reactor Stations Automated multi-vessel workstations [49] Enables the precise, simultaneous execution of the multiple reaction conditions required by a DoE matrix, ensuring consistency.
Analytical Standards & Kits Internal standards, calibrated substrates for HPLC/GC [49] Ensures accurate and reproducible quantification of responses (yield, conversion, selectivity) across all design points.
12-Methylhenicosanoyl-CoA12-Methylhenicosanoyl-CoA, MF:C43H78N7O17P3S, MW:1090.1 g/molChemical Reagent
5'-O-Acetyl Adenosine5'-O-Acetyl Adenosine, MF:C12H15N5O5, MW:309.28 g/molChemical Reagent

The failure of OFAT to identify critical factor interactions is not a minor drawback but a fundamental design flaw that renders it inadequate for optimizing complex, multivariate systems like modern organic syntheses. As demonstrated, this blindness can lead to suboptimal processes, wasted resources, and a lack of fundamental mechanistic understanding. Within the overarching thesis of DoE superiority, the argument is clear: embracing factorial designs, response surface methodologies, and principled statistical analysis is no longer optional for researchers and drug development professionals seeking robust, efficient, and insightful outcomes. The experimental protocols, visual workflows, and toolkit outlined herein provide a pathway to move beyond OFAT's limitations and harness the full power of interactive effects in chemical research.

Avoiding Suboptimal Conditions and Inefficient Resource Use

The pursuit of optimal reaction conditions is a fundamental challenge in organic synthesis, directly impacting efficiency, cost, and sustainability. Traditional One-Factor-at-a-Time (OFAT) methodologies, while intuitive, often lead to suboptimal outcomes and inefficient resource allocation due to their inability to capture interacting variable effects. This whitepaper establishes that systematic approaches, particularly Design of Experiments (DoE), provide a scientifically superior framework for navigating complex reaction parameter spaces. When augmented with machine learning (ML) algorithms, DoE enables researchers to correlate reaction conditions directly with functional performance metrics, achieving outcomes unattainable through conventional optimization strategies and significantly advancing green chemistry principles in pharmaceutical development.

The development of robust and efficient synthetic methodology forms the cornerstone of research in pharmaceuticals, materials science, and agrochemicals. The choice of optimization strategy directly influences not only reaction yield but also resource consumption, waste production, and ultimately the practical adoption of new methodologies. For decades, the one-factor-at-a-time (OFAT) approach has been the de facto standard in many academic laboratories, primarily due to its straightforward implementation and low conceptual barrier. However, this method operates on the flawed assumption that reaction variables act independently, an assumption that frequently breaks down in complex chemical systems. The failure to detect factor interactions leads to identification of local, rather than global, optima and results in processes that are inherently suboptimal. In contrast, systematic approaches like Design of Experiments (DoE) employ statistical principles to vary multiple factors simultaneously, thereby mapping the reaction landscape comprehensively and identifying true optimal conditions. For drug development professionals, the transition from OFAT to DoE and ML-enhanced optimization is not merely a technical improvement but a strategic necessity for reducing development timelines, minimizing material consumption, and implementing greener processes.

Theoretical Foundations: OFAT Limitations and DoE Advantages

The Scientific and Statistical Pitfalls of OFAT

The OFAT approach, while simple in concept, contains fundamental methodological flaws that limit its effectiveness for optimizing complex processes:

  • Failure to Detect Interactions: OFAT is inherently incapable of detecting interactions between factors, such as when the optimal level of one reagent depends on the concentration of another. This frequently leads to incorrect conclusions about a system's behavior [9].
  • Inefficient Resource Use: Exploring multiple variables via OFAT requires a disproportionately large number of experiments compared to DoE. For instance, examining just 5 factors at 3 levels each requires 3⁵ = 243 experiments in OFAT versus as few as 16-46 runs with appropriate DoE designs [9] [12].
  • False Optima Identification: As demonstrated in Figure 1, OFAT can easily miss the true optimum conditions when interactions between variables exist. A hypothetical optimization shows how varying temperature while keeping reagent equivalents constant (and vice versa) identifies a local optimum at T=55°C with 2 equivalents, completely missing the global optimum at T=105°C with only 1.25 equivalents [9].
The DoE Paradigm: A Systematic Framework

Design of Experiments addresses OFAT's limitations through statistical principles that provide a robust framework for efficient experimentation:

  • Simultaneous Factor Variation: By deliberately varying multiple factors simultaneously according to predefined matrices (e.g., full factorial, Taguchi arrays), DoE can directly quantify both main effects and factor interactions with far greater efficiency [9].
  • Model Building and Prediction: DoE generates mathematical models that describe how factors influence responses, enabling prediction of outcomes across the experimental space and accurate identification of optimal regions [3].
  • Built-in Quality Control: The statistical foundation of DoE includes replication points and center points that provide inherent quality checks, allowing researchers to assess reproducibility and curvature effects without additional dedicated experiments [9].

Table 1: Fundamental Differences Between OFAT and DoE Approaches

Characteristic OFAT Approach DoE Approach
Factor Handling Varies one factor while holding others constant Varies multiple factors simultaneously
Interaction Detection Incapable of detecting factor interactions Explicitly quantifies interactions between factors
Experimental Efficiency Low: Requires many runs for multiple factors High: Explores factor space with minimal runs
Statistical Robustness Low: No inherent replication or error estimation High: Includes replication and center points
Optimum Identification Often finds local rather than global optima Systematically maps entire space to find global optimum
Model Development No predictive model generated Creates predictive mathematical models

Implementing DoE in Research: Methodologies and Protocols

Core Experimental Design and Workflow

Successful implementation of DoE follows a structured workflow that ensures comprehensive exploration of the experimental parameter space:

G Start Define Optimization Objectives F1 Identify Critical Factors and Ranges Start->F1 F2 Select Appropriate DoE Design F1->F2 F3 Execute Experimental Runs F2->F3 F4 Analyze Data and Build Model F3->F4 F5 Verify Model with Validation Experiments F4->F5 F5->F2 If model inadequate End Implement Optimal Conditions F5->End

DoE Implementation Workflow

The process begins with clearly defining the objectives and key responses to be optimized (e.g., yield, purity, cost). Researchers must then identify the critical factors to be studied and their realistic ranges based on mechanistic understanding or preliminary data. The selection of an appropriate experimental design depends on the number of factors, the need to estimate interactions, and the suspected complexity of the response surface [12]. For instance, a recent study comparing 31 different DoE designs found that Central Composite Designs (CCD) and certain Taguchi arrays provided excellent characterization of complex systems with significant nonlinearity [12].

Detailed Protocol: DoE Optimization of Macrocyclization Reaction

The following protocol adapts a published procedure for DoE optimization of Yamamoto macrocyclization, demonstrating how reaction conditions can be correlated directly with device performance in organic light-emitting devices (OLEDs) [13]:

Experimental Objective: Optimize a macrocyclization reaction yielding a mixture of methylated [n]cyclo-meta-phenylenes ([n]CMPs) for direct application in OLED fabrication without purification.

Factors and Levels:

  • M: Equivalents of Ni(cod)â‚‚ (Levels: 1.5, 1.75, 2.0)
  • T: Dropwise addition time of dihalotoluene 1 (Levels: 6, 9, 12 hours)
  • C: Final concentration of 1 (Levels: 0.025, 0.050, 0.075 M)
  • R: % content of bromochlorotoluene (1b) in 1 (Levels: 20%, 50%, 80%)
  • S: % content of DMF in solvent (Levels: 20%, 50%, 80%)

Experimental Design:

  • Select an L18 (2¹ × 3⁷) Taguchi orthogonal array to accommodate 5 factors at 3 levels with only 18 experimental runs [13].
  • Prepare reaction mixtures according to the designated factor combinations in oven-dried reaction vessels under inert atmosphere.
  • Conduct macrocyclization reactions using the specified conditions with thorough stirring.
  • Upon completion, work up reactions by standard aqueous extraction and pass through short-path silica gel to remove metal residues and polar byproducts.
  • Analyze crude products by MALDI-MS to determine distribution of [n]CMP congeners.
  • Fabricate OLED devices by spin-coating solutions of crude reaction mixtures mixed with Ir emitter (14 wt% in layer) to form emission layers (20 nm), followed by sublimation of TPBi as electron transport layer (60 nm).
  • Evaluate device performance by measuring external quantum efficiency (EQE) in quadruplicate for each set of conditions.

Machine Learning Integration:

  • Apply Support Vector Regression (SVR), Partial Least Squares Regression (PLSR), and Multilayer Perceptron (MLP) to model the relationship between reaction factors and EQE performance.
  • Validate models using leave-one-out cross-validation (LOOCV), selecting SVR based on lowest mean square error (MSE: SVR = 0.0368, PLSR = 0.0396, MLP = 0.2606) [13].
  • Generate predictive heatmaps to identify optimal factor combinations for maximum EQE.
  • Verify model predictions with test runs, achieving experimental EQE of 9.6% versus predicted 11.3% at optimal conditions [13].

Table 2: Representative DoE Experimental Matrix and Results for Macrocyclization Optimization

Run Ni(cod)â‚‚ (equiv) Addition Time (h) Concentration (M) Br/Cl Ratio (%) DMF (%) EQE (%)
1 1.5 6 0.025 20 20 6.2
2 1.5 9 0.050 50 50 8.1
3 1.5 12 0.075 80 80 5.7
4 1.75 6 0.050 80 20 7.5
5 1.75 9 0.075 20 50 8.9
6 1.75 12 0.025 50 80 7.2
7 2.0 6 0.075 50 20 8.5
8 2.0 9 0.025 80 50 9.6
9 2.0 12 0.050 20 80 7.8
Advanced Application: DoE for Solvent Optimization

Solvent selection represents a particularly challenging optimization problem due to the multidimensional nature of solvent properties. DoE addresses this through principle component analysis (PCA) to create solvent maps:

  • Solvent Space Mapping: PCA reduces 136 solvents with diverse properties to a 2D map where position reflects combined physicochemical characteristics [9].
  • Strategic Selection: Choose solvents from different regions of the PCA map (vertices and center) to maximally explore solvent property space with minimal experiments.
  • Model Application: The resulting model identifies optimal solvent regions and suggests safer, more sustainable alternatives to traditional hazardous solvents [9].

Comparative Analysis: OFAT versus DoE Performance Metrics

The performance advantages of DoE over OFAT become particularly evident when examining specific case studies across different chemical domains:

Case Study 1: Macrocyclization for OLED Materials The DoE+ML approach applied to Yamamoto macrocyclization identified optimal conditions that produced a mixture of [n]CMP congeners which, when used directly without purification in OLED devices, achieved an external quantum efficiency (EQE) of 9.6% [13]. This performance surpassed devices fabricated with purified single compounds ([5]CMP: EQE = 0.9%; [6]CMP: EQE = 0.8%), demonstrating that DoE could identify synergistic effects in complex mixtures that OFAT would typically miss [13]. The DoE approach required only 18 carefully designed experiments to optimize 5 factors across 3 levels each—a parameter space that would require 243 experiments using OFAT.

Case Study 2: Thermal Characterization of Building Materials A comprehensive study comparing 31 different DoE designs for characterizing the thermal performance of a double-skin façade found that certain designs (e.g., CCD, specific Taguchi arrays) provided excellent characterization efficiency, while others failed to adequately capture the system behavior [12]. This highlights that proper DoE selection is critical and should be based on the suspected extent of nonlinearity and factor interactions in the system under investigation [12].

Table 3: Quantitative Performance Comparison of OFAT versus DoE in Published Studies

Optimization Metric OFAT Performance DoE Performance Improvement
Experimental Efficiency 243 runs for 5 factors at 3 levels 18 runs for 5 factors at 3 levels 93% reduction in experimental load
OLED Device Performance 0.9% EQE (purified [5]CMP) 9.6% EQE (optimized mixture) 10.7x efficiency increase
Resource Utilization High (requires separation/purification) Low (crude mixture directly usable) Elimination of purification steps
Process Sustainability Higher waste generation Minimal waste production Greener chemistry principles
Predictive Capability No model for prediction Accurate SVR model (MSE = 0.0368) Enables future optimization

The Scientist's Toolkit: Essential Research Reagent Solutions

Implementing effective DoE strategies requires both methodological expertise and appropriate practical tools. The following table details key reagents and materials essential for successful experimental optimization:

Table 4: Essential Research Reagent Solutions for Optimization Studies

Reagent/Material Function in Optimization Application Notes
Taguchi Orthogonal Arrays Predefined experimental matrices that maximize information with minimal runs Ideal for screening multiple factors (5-7) simultaneously; L18 array used in macrocyclization study [13]
Solvent Property Databases Collections of solvent parameters for PCA-based solvent selection Enables rational solvent optimization using solvent maps; incorporates 136 solvents with diverse properties [9]
Support Vector Regression (SVR) Machine learning algorithm for modeling complex factor-response relationships Superior performance for chemical optimization (MSE = 0.0368 vs MLP = 0.2606) [13]
Anhydrous Solvents Ensure reproducibility in air/moisture sensitive reactions Tetrahydrofuran (distilled from Na/benzophenone), diethyl ether (purified through alumina), pyridine (stored over KOH) [57] [58]
Internal Standards for qNMR Quantitatively determine reaction yield and purity Dimethyl fumarate used for qNMR purity determination of silane products [57]
3-Hydroxy-2-methylhexanoyl-CoA3-Hydroxy-2-methylhexanoyl-CoA, MF:C28H48N7O18P3S, MW:895.7 g/molChemical Reagent
trans-12,13-Epoxy-9(Z)-octadecenoic acidtrans-12,13-Epoxy-9(Z)-octadecenoic acid, MF:C18H32O3, MW:296.4 g/molChemical Reagent

Technological Frontiers: Machine Learning and Self-Optimizing Systems

The integration of machine learning with DoE represents the cutting edge of reaction optimization, enabling predictive models that become increasingly accurate with data accumulation:

G ML1 High-Throughput Experimentation (HTE) ML2 Database Curation and Management ML1->ML2 ML3 Machine Learning Model Training ML2->ML3 ML4 DoE + ML Prediction ML3->ML4 ML5 Optimal Condition Identification ML4->ML5 ML5->ML1 Data feedback loop

DoE and ML Integration Framework

  • Multi-Objective Optimization: Advanced algorithms can simultaneously optimize conflicting objectives (e.g., yield, cost, safety, purity) by applying appropriate weighting factors to balance these priorities [3].
  • Self-Optimizing Systems: Automated platforms combine DoE, continuous flow reactors, and inline analytics to create closed-loop systems that autonomously explore parameter spaces and converge on optimal conditions with minimal researcher intervention [3].
  • High-Throughput Experimentation: Miniaturized screening platforms (e.g., 1536-well microtiter plates) generate extensive datasets for ML training, though these typically require automation infrastructure for reliable operation [3].
  • Cross-Reaction Prediction: Early demonstrations show neural networks can predict optimal conditions (catalysts, solvents, reagents, temperature) for unfamiliar reactions with approximately 50% accuracy in top-3 predictions, establishing the foundation for transfer learning in chemical optimization [3].

The methodological evolution from OFAT to DoE and ML-enhanced optimization represents a paradigm shift in how synthetic chemists approach reaction development. The evidence clearly demonstrates that systematic approaches outperform traditional OFAT methodology in efficiency, performance outcomes, and sustainability metrics. For researchers and drug development professionals, adopting these methodologies requires an initial investment in learning statistical concepts and experimental design principles, but the return on this investment manifests as reduced development timelines, decreased material consumption, and identification of superior conditions that would remain inaccessible through OFAT approaches. As optimization technologies continue advancing, particularly through increased automation and machine learning integration, the capability to navigate complex chemical spaces will become increasingly sophisticated, further accelerating the discovery and development of novel molecular entities for pharmaceutical applications.

Leveraging Response Surface Methodology (RSM) for Precise Optimization

In organic synthesis research, the traditional approach to optimization has long been the One-Factor-at-a-Time (OFAT) method. While straightforward and widely taught, OFAT involves changing a single variable while holding all others constant, creating a narrow experimental focus that inevitably fails to identify interactions between factors and may miss the true optimal solution [6]. This approach provides limited coverage of the experimental space and represents an inefficient use of valuable resources [6]. In drug development, where multiple parameters—such as temperature, concentration, catalyst equivalents, and solvent composition—can interact in complex ways, OFAT's limitations become particularly problematic, potentially leading to suboptimal processes that fail in scale-up.

Response Surface Methodology (RSM) represents a fundamental shift from this traditional approach. As a powerful statistical tool within the Design of Experiments (DoE) framework, RSM uses mathematical and statistical techniques to model and analyze problems with multiple influencing factors [38]. By systematically exploring the relationship between several explanatory variables and one or more response variables, RSM enables researchers to establish cause-and-effect relationships and identify the factor level combinations that yield optimum performance [38] [25]. This methodology has proven particularly valuable in organic synthesis and pharmaceutical development, where relationships between variables and outcomes are often complex and poorly understood, making traditional optimization challenging [38].

Table 1: Fundamental Differences Between OFAT and RSM Approaches

Characteristic OFAT (One-Factor-at-a-Time) RSM (Response Surface Methodology)
Experimental Strategy Vary one factor while holding others constant Systematically vary multiple factors simultaneously
Interaction Detection Cannot detect factor interactions Explicitly models and identifies interactions
Efficiency Inefficient use of experimental resources Establishes optimal conditions with minimal resources
Experimental Space Coverage Limited coverage Comprehensive coverage of multidimensional space
Underlying Model No comprehensive model Empirical model relating factors to responses
Optimal Solution May miss true optimum Systematically locates region of optimum response

Fundamental Principles of Response Surface Methodology

Core Concepts and Terminology

RSM is built upon several fundamental statistical and mathematical concepts that are essential for proper implementation and interpretation. At its core, RSM examines the connections between multiple influencing factors and related outcomes to develop an empirical model that accurately represents what's happening in a process or system [38].

Key concepts include:

  • Factors and Levels: Factors are the independent input variables that can be controlled and manipulated during experimentation (e.g., temperature, pH, concentration). Each factor is tested at different "levels"—specific settings or values that define the experimental range [59].
  • Responses: These are the dependent output variables or measurable results that represent the performance measures of interest (e.g., yield, purity, efficiency) [59].
  • Experimental Design: RSM relies on structured experimental designs that allow for planned changes to input factors to observe corresponding changes in outputs. These designs enable efficient exploration of the factor space [38].
  • Regression Analysis: RSM heavily utilizes regression analysis techniques like multiple linear regression and polynomial regression to model the functional relationship between responses and independent input variables [38].
  • Response Surface Models: The ultimate objective is to generate a mathematical relationship that describes how input variables influence the response(s) of interest, typically using first-order or second-order polynomial equations [38].
The Sequential Nature of RSM

A key strength of RSM lies in its sequential approach to optimization [25]. The methodology typically follows a structured path:

  • Screening Experiments: Initial experiments to identify the most influential factors from a larger set of potential variables.
  • Method of Steepest Ascent/Descent: Once significant factors are identified, this method efficiently moves from the current operating conditions toward the optimum region [25] [24].
  • Detailed Optimization: When near the optimum, a more elaborate model (typically second-order) is fitted to precisely characterize the response surface and locate the optimum [25].

This sequential approach allows researchers to efficiently navigate complex experimental spaces, focusing resources on the most promising regions for optimization.

rsm_sequence Start Initial Operating Conditions Screening Screening Experiments (Identify Key Factors) Start->Screening SteepestAscent Steepest Ascent/Descent (Move Toward Optimum) Screening->SteepestAscent RegionDetection Curvature Detection (Near Optimum?) SteepestAscent->RegionDetection RegionDetection->SteepestAscent No Significant Curvature Optimization RSM Optimization (Fit Second-Order Model) RegionDetection->Optimization Curvature Detected Validation Model Validation & Confirmation Optimization->Validation

Implementing RSM: A Step-by-Step Experimental Guide

Preliminary Screening and Factor Selection

The initial phase of any RSM study involves identifying the critical factors that significantly influence the response variables. While prior knowledge and theoretical understanding can guide this selection, screening designs such as fractional factorials or Plackett-Burman designs are particularly valuable when dealing with many potential factors [59]. These designs efficiently identify the few important factors from many potential variables, allowing researchers to focus subsequent optimization efforts on the most influential parameters.

For example, in optimizing a macrocyclization reaction for organic light-emitting devices, researchers initially identified five potentially influential factors: Ni(cod)2 equivalents, dropwise addition time, final concentration, bromochlorotoluene content, and DMF percentage in solvent [13]. Using a Taguchi orthogonal array design, they were able to systematically evaluate these factors and their impact on device performance.

The Method of Steepest Ascent

Once significant factors are identified, the method of steepest ascent provides a systematic procedure for moving from the current operating conditions toward the region of the optimum response [25] [24]. This approach utilizes a first-order model:

[y = \beta0 + \beta1x1 + \beta2x_2 + \varepsilon]

The coefficients of this model ((\beta1), (\beta2)) determine the path of steepest ascent—the direction in which the response increases most rapidly [24]. Experiments are conducted along this path until the response no longer improves, indicating the vicinity of the optimum has been reached.

A chemical process optimization example demonstrates this approach: when yield was found to be a function of reaction temperature and time, the fitted first-order model was (\hat{y} = 40.34 + 0.775x1 + 0.325x2), indicating the path of steepest ascent required moving 1.1625 units in the x1 direction for every 0.4875 units in the x2 direction [24]. By following this path with appropriate step sizes, the experimenter efficiently located the region of maximum yield.

Response Surface Designs and Modeling

When near the optimum region, as indicated by a significant curvature effect, a more elaborate second-order model is required to accurately capture the response surface [25] [24]. The general form of this model for k factors is:

[y = \beta0 + \sum{i=1}^k \betaixi + \sum{i=1}^k \beta{ii}xi^2 + \sum{i{ij}xix_j + \varepsilon]}\sum>

Special experimental designs are used to efficiently estimate the parameters of this second-order model:

  • Central Composite Designs (CCD): These consist of a two-level factorial design augmented by center points and axial points, allowing estimation of all quadratic terms [24].
  • Box-Behnken Designs: These are three-level designs that are particularly efficient for fitting second-order models, often requiring fewer runs than central composite designs [60].

For example, in optimizing silica extraction from rice husk and straw ash, researchers employed a central composite design to study the effects of sodium hydroxide concentration, temperature, and digestion time [61]. This approach allowed them to efficiently model the quadratic response surface and identify optimal processing conditions.

Table 2: Common RSM Experimental Designs and Applications

Design Type Structure Number of Runs (3 factors) Best Use Cases
Central Composite Design (CCD) Factorial + center points + axial points 15-20 General optimization; can be rotatable
Box-Behnken Design Three-level incomplete factorial 13-15 Efficient quadratic modeling
Three-Level Full Factorial All combinations of 3 levels per factor 27 Comprehensive but resource-intensive
Model Validation and Optimization

After developing the response surface model, it's crucial to validate model adequacy using statistical tests like analysis of variance (ANOVA), lack-of-fit tests, R-squared values, and residual analysis [38]. Once validated, the model can be used to locate the optimum operating conditions through techniques like canonical analysis or numerical optimization [38].

In the OLED material optimization study, researchers validated their response surface model using leave-one-out cross-validation and confirmation experiments [13]. The support vector regression model successfully predicted external quantum efficiency with a mean square error of 0.0368, and confirmation runs at predicted optimum conditions yielded performance values that closely matched predictions (9.6% experimental vs. 11.3% predicted) [13].

Advanced RSM Applications in Organic Synthesis and Drug Development

Case Study: OLED Material Optimization

A compelling application of RSM in complex organic synthesis demonstrates the methodology's power beyond simple optimization. Researchers sought to optimize the performance of organic light-emitting devices (OLEDs) by correlating reaction conditions directly with device performance [13]. Rather than focusing solely on reaction yield, they used a DoE + machine learning approach to connect five reaction factors (Ni(cod)2 equivalents, addition time, concentration, bromochlorotoluene content, and DMF percentage) directly with the external quantum efficiency of the final devices [13].

This approach eliminated energy-consuming separation and purification steps, aligning with green chemistry principles while achieving a remarkable device performance of 9.6% external quantum efficiency—surpassing the performance achievable with purified materials [13]. The success of this "from-flask-to-device" optimization highlights RSM's ability to navigate complex multivariate spaces in pharmaceutical and materials development.

Case Study: Adsorbent Material Synthesis and Dye Removal

In environmental applications relevant to pharmaceutical manufacturing, researchers employed RSM to optimize the synthesis of low-cost metal-organic frameworks (MOFs) from melamine and bauxite for efficient removal of bromocresol green dye from water [62]. Using RSM with an I-optimal and quadratic model, they systematically investigated the impact of pH, adsorbent dose, concentration, time, and temperature on dye removal efficiency [62].

The study identified optimal conditions (acidic pH, 0.024 g adsorbent dose, 18.8 ppm concentration, 90 minutes, and 15°C) and revealed that the adsorption process followed Langmuir isotherm and pseudo-second-order kinetics, with spontaneous and endothermic characteristics [62]. This comprehensive optimization demonstrates RSM's utility in developing sustainable materials for environmental remediation—a concern increasingly important in pharmaceutical manufacturing.

workflow Problem Define Problem & Response Variables Screen Screen Potential Factor Variables Problem->Screen Design Select RSM Design (CCD, Box-Behnken) Screen->Design Experiment Conduct Experiments According to Design Design->Experiment Model Develop Response Surface Model Experiment->Model Validate Check Model Adequacy Model->Validate Optimize Optimize & Validate Optimum Conditions Validate->Optimize

Analytical Method Development

In pharmaceutical analysis, RSM has proven valuable for developing robust analytical methods. One study optimized a miniaturized metal-organic framework based pipette-tip solid phase extraction method for analyzing dyes in seawater samples [60]. The researchers used RSM based on a Box-Behnken design to efficiently optimize multiple parameters simultaneously: pH, salt amount, eluent solvent type and volume, surfactant concentration, sample volume, and extraction/desorption cycles [60].

The optimized method achieved impressive sensitivity with detection limits of 0.09-0.38 µg/L and reproducibility better than 6.4% RSD [60]. This application demonstrates RSM's superiority over OFAT in developing robust analytical methods where multiple interacting factors can affect performance—a common scenario in pharmaceutical quality control and method validation.

Essential Research Reagent Solutions for RSM Studies

Successful implementation of RSM in organic synthesis requires careful selection of reagents and materials. The following table summarizes key components used in representative RSM-optimized studies:

Table 3: Essential Research Reagent Solutions for RSM-Optimized Synthesis

Reagent/Material Function in Optimization Application Example
Metal-Organic Frameworks (MOFs) Porous adsorbent material with tunable properties Bromocresol green dye removal from water [62]
Ni(cod)â‚‚ Catalyst Cross-coupling catalyst for macrocyclization Yamamoto coupling for OLED material synthesis [13]
Rice Husk/Rice Straw Ash Sustainable silica source Biogenic silica extraction [61]
Co-MOF Adsorbent Solid phase extraction sorbent Pipette-tip SPE of dyes for HPLC analysis [60]
Triton X-114 Surfactant Cloud point extraction mediator Dye extraction and pre-concentration [60]
Sodium Hydroxide (NaOH) Alkaline digestion agent Silica extraction from agricultural waste [61]

Response Surface Methodology represents a paradigm shift from traditional OFAT approaches in organic synthesis and drug development. By enabling systematic investigation of multiple factors and their interactions, RSM provides a powerful framework for efficient process optimization. The methodology's sequential nature—progressing from screening to steepest ascent to detailed optimization—ensures efficient use of resources while comprehensively exploring complex experimental spaces.

As the case studies in OLED material development, adsorbent optimization, and analytical method development demonstrate, RSM enables researchers to navigate multivariate systems effectively, often revealing optimal conditions that would remain undiscovered through OFAT approaches. Furthermore, the integration of RSM with machine learning techniques represents an emerging frontier that enhances predictive capability and optimization efficiency [13].

For researchers in pharmaceutical development and organic synthesis, embracing RSM facilitates not only more efficient optimization but also deeper process understanding—a crucial advantage in quality by design (QbD) initiatives and regulatory submissions. By moving beyond the limitations of OFAT, RSM empowers scientists to develop more robust, efficient, and sustainable synthetic processes that meet the evolving challenges of modern drug development.

In the competitive landscape of drug development and organic synthesis, researchers face the persistent challenge of optimizing chemical reactions across multiple, often competing, objectives. The traditional approach, One-Factor-at-a-Time (OFAT), involves varying a single parameter while holding all others constant. While intuitively simple, this method possesses fundamental limitations for modern synthesis challenges, particularly when striving to balance critical responses like yield, selectivity, and cost simultaneously [2] [32]. OFAT experimentation fails to account for interaction effects between factors, potentially leading to misleading conclusions and suboptimal process conditions [2] [9]. This article frames these methodologies within the broader thesis of Design of Experiments (DoE) versus OFAT, demonstrating how a systematic DoE approach enables researchers to navigate complex multi-response landscapes efficiently, uncovering optimal conditions that traditional methods overlook.

The pursuit of a new chemical entity does not end with its discovery but extends into optimizing its synthesis for scale-up and manufacturing. Here, the limitations of OFAT become particularly pronounced. A process optimized for maximum yield via OFAT might require prohibitively expensive reagents or generate excessive waste, conflicting with cost and environmental objectives [63]. Similarly, conditions that maximize yield might compromise selectivity, leading to problematic impurities. The paradigm is shifting from this sequential, one-dimensional optimization to a multivariate approach where DoE, often enhanced with machine learning (ML), allows for the synchronous optimization of multiple variables and responses [63]. This guide provides a technical foundation for implementing such strategies, equipping scientists with the methodologies to enhance both the efficiency and sustainability of their research.

OFAT vs. DoE: A Fundamental Paradigm Clash

Core Principles and Limitations of OFAT

The OFAT approach is deeply entrenched in many scientific disciplines due to its straightforward nature. It involves systematically changing one input variable (e.g., temperature) across a range of values while maintaining all other parameters (e.g., catalyst loading, solvent, concentration) at fixed levels [2]. After identifying the apparent best level for the first variable, the experimenter moves to the next factor, holding the first at its new "optimal" level. This process continues until all factors of interest have been tested.

However, this methodology contains critical flaws for complex systems:

  • Inability to Detect Interactions: OFAT assumes that factors are independent, an assumption often violated in chemical systems. If the effect of temperature on yield depends on the catalyst loading (an interaction), OFAT cannot detect this relationship [2] [64]. The identified "optimum" may therefore be a local, not global, optimum, as illustrated in Figure 1.
  • Inefficiency and Resource Intensity: Exploring factors sequentially requires a large number of experiments, making it time-consuming and costly, especially with many factors [2] [32]. For example, a process with 5 continuous factors can take 46 runs with OFAT, whereas a comparable DoE may require only 12-27 runs [32].
  • Missed Optimal Conditions: OFAT provides limited coverage of the experimental space. Simulations demonstrate that OFAT finds the true process sweet spot only about 25-30% of the time, meaning it frequently settles for suboptimal conditions [32].

The DoE Advantage for Multi-Response Optimization

Design of Experiments is a structured, statistical method for simultaneously investigating the effects of multiple input factors on one or more responses. Unlike OFAT, DoE is founded on principles of randomization, replication, and blocking to ensure robust and reproducible results [2]. Its advantages for multi-response problems are profound:

  • Efficient Exploration of Factor Space: DoE uses carefully designed arrays of experimental runs that efficiently span the multi-dimensional factor space. This allows for the extraction of maximum information—main effects, interaction effects, and even quadratic effects—from a minimal number of experiments [2] [65].
  • Modeling of Interaction Effects: A key strength of DoE is its ability to quantify how factors interact. This is crucial when optimizing for conflicting responses, as a change that benefits yield might detrimentally impact selectivity; these trade-offs are only visible through interaction studies [64] [9].
  • Built-in Optimization Capabilities: Using techniques like Response Surface Methodology (RSM), DoE can build mathematical models that predict response outcomes for any combination of factor levels within the studied range [2] [66]. This model enables direct multi-response optimization to find a factor setting that best balances all critical criteria, such as maximizing yield and selectivity while minimizing cost.

Table 1: Comparison of OFAT and DoE Characteristics

Characteristic OFAT Approach DoE Approach
Experimental Strategy Sequential, one-dimensional Simultaneous, multi-dimensional
Factor Interactions Not detectable Quantifiable and analyzable
Experimental Efficiency Low; requires many runs for multiple factors High; information-rich with fewer runs
Primary Focus Finding a single "best" setting Mapping the entire experimental space
Model Building Not possible; no structured approach Creates a predictive cause-effect model [64]
Handling Multiple Responses Conditional, manual comparison Automated, via multi-variable optimization [64]
Identification of True Optimum Unreliable; finds local optimum ~25% of the time [32] Reliable; systematically finds global optimum

DoE Methodologies for Multi-Response Problems

Foundational DoE Designs

Implementing a successful DoE strategy begins with selecting an appropriate experimental design based on the project's goals. Screening designs are used to identify the most influential factors from a large set, while optimization designs characterize the response surface in detail.

  • Factorial Designs: These are the cornerstone of DoE. A full factorial design tests all possible combinations of factors and their levels. For example, a 2^3 factorial design investigates three factors, each at two levels (high/low), in 8 experimental runs. This design estimates all main effects and all interaction effects between factors, providing a complete picture of the factor influences without confounding [2].
  • Fractional Factorial Designs: When the number of factors is large (e.g., 5 or more), full factorial designs become prohibitively large. Fractional factorial designs strategically select a subset (a fraction) of the full factorial runs. While this sacrifices the ability to estimate some higher-order interactions, it efficiently identifies the most critical main effects and low-order interactions, making it ideal for screening [66].
  • Response Surface Designs: Once the critical factors are identified, Response Surface Methodology (RSM) designs are employed to model curvature and find the optimal factor settings. Central Composite Designs (CCD) and Box-Behnken Designs (BBD) are two common types that efficiently fit a second-order (quadratic) model to the data [2] [66]. This model is essential for predicting a maximum (e.g., for yield) or a minimum (e.g., for cost).

The Experimental Workflow: From Design to Optimization

A structured workflow is key to a successful DoE campaign, especially when juggling multiple responses. The process, as outlined in recent literature on organic synthesis optimization [63], can be summarized in the following workflow:

workflow Problem Formulation Problem Formulation Experimental Design Experimental Design Problem Formulation->Experimental Design High-Throughput Execution High-Throughput Execution Experimental Design->High-Throughput Execution Data Collection & Analysis Data Collection & Analysis High-Throughput Execution->Data Collection & Analysis Model Building & Validation Model Building & Validation Data Collection & Analysis->Model Building & Validation Multi-Response Optimization Multi-Response Optimization Model Building & Validation->Multi-Response Optimization Verification Experiment Verification Experiment Multi-Response Optimization->Verification Experiment

Figure 1: DoE Multi-Response Optimization Workflow

  • Problem Formulation & Objective Definition: Clearly define the goal. For a synthesis, this could be "maximize yield (>85%), maintain selectivity (>95%), and minimize raw material cost." Identify all potential input factors (e.g., temperature, time, catalyst loading, solvent, reagent equivalents) and the responses to be measured [65] [63].
  • Experimental Design Selection: Choose a design aligned with the objective. A Plackett-Burman or fractional factorial design is suitable for screening many factors. A CCD or BBD is used for optimization after key factors are known [66].
  • High-Throughput Execution (where applicable): Leverage automated platforms, such as Chemspeed systems or custom robotic setups, to execute the designed experiments with high precision and reproducibility. This is particularly valuable for exploring complex, multi-factor spaces rapidly [63].
  • Data Collection & Analysis: Run the experiments in a randomized order to avoid systematic bias. Collect accurate data for all predefined responses. Use statistical software (e.g., JMP, Minitab, ValChrom) to perform Analysis of Variance (ANOVA) and determine the statistical significance of each effect [65] [32].
  • Model Building & Validation: For each response, develop a mathematical model (e.g., a polynomial equation) that relates the factors to the response. Check the model's adequacy using statistical measures (R², adjusted R², prediction error) and run confirmation experiments at predicted points to validate the model [66].
  • Multi-Response Optimization: This is the critical step. Use the validated models for yield, selectivity, and cost simultaneously. Employ numerical optimization techniques (e.g., desirability functions or simplex algorithms) to find a factor setting that provides the best overall compromise, satisfying the constraints for all responses [64] [63]. The output is often a "sweet spot" region or a set of optimal conditions.

Practical Application: Protocols and a Case Framework

The Scientist's Toolkit: Essential Reagents and Materials

Table 2: Key Research Reagent Solutions for DoE in Synthesis

Reagent/Material Function in DoE Context Multi-Response Consideration
Solvent Library [9] To explore "solvent space" as a categorical factor, influencing reaction kinetics, solubility, and mechanism. Different solvents can drastically affect both yield and selectivity, and vary greatly in cost and environmental impact.
Catalyst Systems To test different catalytic entities (e.g., Pd, Cu, organocatalysts) and their loadings. Catalyst choice and loading are primary drivers for yield and selectivity, and a major contributor to overall cost.
Reagent Equivalents To vary the stoichiometry of reactants, oxidants, or reducing agents. Optimizing equivalents directly balances yield against cost and can influence selectivity by reducing side reactions.
High-Throughput Reaction Blocks [63] To perform multiple experiments in parallel (e.g., in 24- or 96-well plates), ensuring consistency and efficiency. Enables rapid data generation for all responses (yield, selectivity) under systematically varied conditions.
N-Hexanoyl-biotin-lactosylceramideN-Hexanoyl-biotin-lactosylceramide, MF:C46H82N4O15S, MW:963.2 g/molChemical Reagent
Firefly luciferase-IN-5Firefly luciferase-IN-5, MF:C23H24N4O3S, MW:436.5 g/molChemical Reagent

Generic Experimental Protocol for a DoE Optimization Study

The following protocol outlines a generalized step-by-step procedure for optimizing a synthetic reaction using a Response Surface Design, adaptable for reactions like aminations or cross-couplings [63] [9].

Objective: To maximize yield and selectivity while minimizing cost for a model transformation. Critical Factors Identified from Screening: Temperature (°C), Catalyst Loading (mol%), and Reaction Time (hours).

Step 1: Experimental Design

  • Using statistical software, select a Box-Behnken Design (BBD) for 3 factors. This design requires 13 experiments, including 5 center points for estimating curvature and experimental error.
  • Define the factor ranges based on prior knowledge: Temperature (60-100°C), Catalyst Loading (1-5 mol%), Time (2-12 hours).
  • The software will generate a randomized run order to minimize bias.

Step 2: Reaction Setup

  • Prepare stock solutions of the substrate and catalyst to ensure accurate and rapid dispensing for all experiments.
  • In a series of 16 reaction vials (allowing for replicates), add the substrate solution according to the experimental plan.
  • Under an inert atmosphere, add the specified volume of catalyst stock solution to each vial as per the design matrix.
  • Add the chosen solvent (fixed for this design, but could be a factor in a broader study) [9].
  • Seal the vials and place them in a pre-heated parallel reactor block capable of maintaining the precise temperatures required by the design.

Step 3: Execution and Work-up

  • Initiate the reactions simultaneously according to the randomized run order.
  • After the specified time for each vial, remove it from the heat and cool rapidly to quench the reaction.
  • Work up each reaction mixture identically (e.g., dilution, extraction).

Step 4: Analysis and Data Collection

  • Analyze each sample using a quantitative analytical method such as HPLC or GC.
  • For each run, calculate and record the three key responses:
    • Yield: Determined by calibrated HPLC/GC against an internal standard.
    • Selectivity: Calculated as the ratio of the desired product peak area to the sum of all product peak areas.
    • Relative Cost: A calculated metric based on the cost of catalyst and reagents used per mole of substrate.

Step 5: Data Analysis and Modeling

  • Input the response data (Yield, Selectivity, Cost) into the statistical software.
  • For each response, perform a multiple regression analysis to fit a quadratic model.
  • Use ANOVA to determine the significance of the model terms. Simplify the model by removing non-significant terms (e.g., using a backward elimination procedure).
  • Validate the model by checking residual plots and, if available, comparing model predictions to the center point replicates.

Step 6: Multi-Response Optimization

  • Use the software's optimization function (e.g., desirability function) to define the goals: Maximize Yield, Maximize Selectivity, and Minimize Cost.
  • The algorithm will search the factor space defined by your models and propose one or more factor combinations that provide the best overall compromise.
  • The output will be a set of optimal conditions, for instance: Temperature = 85°C, Catalyst Loading = 2.5 mol%, Time = 8 hours, with predicted responses of Yield = 88%, Selectivity = 96%, and a 30% reduction in catalyst cost compared to the initial conditions.

Step 7: Verification

  • Conduct at least three verification experiments at the predicted optimal conditions.
  • Compare the measured responses with the model predictions. A close agreement confirms the model's robustness and the success of the optimization.

The transition from OFAT to Design of Experiments represents a fundamental shift in how researchers approach complex optimization challenges in organic synthesis and drug development. While OFAT offers simplicity, it is a risky and inefficient strategy for processes where multiple, interdependent responses like yield, selectivity, and cost are critical. The structured, model-based framework of DoE, particularly when enhanced with modern automation and machine learning, provides a powerful and scientifically rigorous pathway to true process understanding and robust optimization [63].

By adopting DoE, researchers and drug development professionals can move beyond iterative guessing and instead build predictive models that illuminate the entire experimental landscape. This not only accelerates the development timeline and reduces costs but also leads to more sustainable and economically viable chemical processes. In an era of increasing complexity and competition, embracing the multi-response capabilities of DoE is no longer a luxury but a necessity for achieving superior scientific and commercial outcomes.

Integrating Machine Learning with DoE for Enhanced Prediction and Efficiency

The field of organic synthesis research has traditionally relied on the One-Factor-at-a-Time (OFAT) approach to experimentation. While widely taught and straightforward, OFAT offers only limited coverage of the experimental space, often misses optimal solutions, fails to identify interactions between variables, and represents an inefficient use of resources [6]. More significantly, this traditional approach cannot demonstrate the complex interactions between input variables and associated outputs, resulting in the slow and arduous development of new biomaterials and tissue-engineered constructs [67].

Statistically designed experiments, particularly Design of Experiments (DoE), present a fundamental shift from this traditional paradigm. Unlike OFAT, DoE involves varying two or more variables simultaneously to obtain the maximum amount of information from a minimum number of experiments [67]. This approach provides three key advantages: (1) the ability to detect and measure interactions between variables, (2) greater efficiency as each observation provides information about multiple effects, and (3) quantification of experimental error to determine statistical confidence in conclusions [68]. Response Surface Methodology (RSM) represents an advanced form of DoE that uses specially designed arrays for calculating interactions and quadratic responses, effectively producing a 3D image of how multiple factors influence an output simultaneously [69].

The integration of machine learning (ML) with DoE marks the next evolutionary step in experimental design, creating a hybrid approach that lowers costs, accelerates decision-making, and drives more efficient discovery [70]. While conventional DoE ensures balanced coverage of the experimental space when data is scarce, ML builds on those results and any existing data to focus experiments on high-value targets in real-time [70]. This powerful combination is particularly valuable in complex fields such as organic synthesis and drug development, where relationships between variables and outcomes are often unknown or complex, making traditional optimization challenging [38].

Fundamental Concepts: DoE, RSM, and Machine Learning

Design of Experiments and Response Surface Methodology

Response Surface Methodology (RSM) is a powerful statistical tool that uses mathematics and statistics to model problems with multiple influencing factors and their results [38]. Originally developed in the 1950s through pioneering work by mathematicians like Box and Wilson, RSM aims to determine the perfect operational conditions or acceptable performance ranges for a system by mapping input-output relationships visually through response surfaces [38]. The core objective of RSM is to generate a mathematical relationship that describes how input variables influence the response(s) of interest, typically using first-order, second-order polynomial, or quadratic models [38].

The implementation of RSM follows a systematic series of steps [38]:

  • Define the Problem and Response Variables: Clearly articulate the problem statement, goals, and identify critical response variable(s) to optimize.
  • Screen Potential Factor Variables: Identify key input factors that may influence the response(s) through prior knowledge and screening experiments.
  • Code and Scale Factor Levels: Code and scale selected factors to low and high levels spanning the experimental region of interest.
  • Select an Experimental Design: Choose an appropriate experimental design (central composite, Box-Behnken, or D-optimal) based on the number of factors, resources, and objectives.
  • Conduct Experiments: Execute experiments according to the chosen experimental design matrix.
  • Develop the Response Surface Model: Fit a multiple regression model to the experimental data relating the response to the factor variables.
  • Check Model Adequacy: Analyze the fitted model for accuracy and significance using statistical tests like ANOVA, lack-of-fit tests, R² values, and residual analysis.
  • Optimize and Validate the Model: Use optimization techniques to determine factor settings that optimize the response(s) and validate through confirmatory experimental runs.
  • Iterate if Needed: Plan additional experiments in updated regions if the current experimental region is unsatisfactory.
Machine Learning Fundamentals for Experimental Design

Machine learning represents a complementary approach to traditional DoE, defined as a search through a parameter space for a model configuration that minimizes a cost function based on experimental data [71]. While DoE focuses on assessing the influences of treatments and comparing their effects, ML is primarily concerned with making accurate predictions [71]. This fundamental difference in goals leads to distinct emphases: DoE places importance on experimental design to reduce variability in treatment parameter estimates, often within budgetary constraints, while ML emphasizes predictive algorithms and their computational implementation [71].

The primary advantage of machine learning in experimental contexts is its flexibility in handling diverse data types. While DoE approaches are limited to quantitative, countable, or measurable data, ML can process and predict various data forms, including images, video, audio, and high-dimensional data where the number of features exceeds the number of observations [67]. This capability makes ML particularly valuable for complex optimization challenges in fields like tissue engineering and biomaterials science, where multiple characterization techniques generate diverse data types [67].

Table 1: Comparison of Traditional DoE and Machine Learning Approaches

Aspect Traditional DoE Machine Learning
Primary Goal Statistical inference of treatment parameters [71] Accurate predictions [71]
Data Compatibility Quantitative data (number-based, countable, measurable) [67] Images, video, audio, high-dimensional data [67]
Basis Functions Often limited to polynomial models [71] Flexible basis functions (neural networks, SVM, CART ensembles) [71]
Experimental Emphasis Good design to reduce variability [71] Predictive algorithms and computational complexity [71]
Approach to Factors Controlled manipulation with randomization [71] Uses available data without considering production method [71]
The Synergistic Potential of DoE and ML Integration

The integration of DoE and ML creates a synergistic relationship that leverages the strengths of both approaches. DoE provides a structured framework for generating high-quality, representative data through carefully designed experiments, while ML offers powerful tools for extracting complex patterns and relationships from this data that might be missed by traditional statistical models [70]. This combination is particularly effective because ML algorithms, especially supervised learning methods, essentially compute a transfer function of a system given that the training data connects inputs with known outputs [71].

This integrated approach enables what Genentech researchers term a "lab in a loop" mechanism, where data from the lab and clinic are used to train AI models and algorithms, and then the trained models make predictions on drug targets, therapeutic molecules, and other factors [72]. These predictions are tested in the lab, generating new data that helps retrain the models to be even more accurate [72]. This iterative process streamlines the traditional trial-and-error approach for novel therapies and improves model performance across all research programs [72].

Integrated DoE-ML Framework: Methodologies and Experimental Protocols

DoE-ML Integrated Workflow for Experimental Optimization

The integration of DoE and ML follows a systematic workflow that leverages the strengths of both approaches. This integrated framework enables researchers to efficiently explore complex experimental spaces while building accurate predictive models. The workflow incorporates both traditional DoE principles and modern ML capabilities to create an iterative optimization cycle.

Start Define Problem and Response Variables DoE DoE Initial Screening (Factorial Design) Start->DoE ML_Model Develop Initial ML Model DoE->ML_Model RS RSM Optimization (Central Composite/Box-Behnken) ML_Model->RS Update Update ML Model with New Experimental Data RS->Update Validate Validate and Confirm Optimal Conditions Update->Validate Validate->DoE Iterate if Needed End Optimal Solution Identified Validate->End

Diagram 1: DoE-ML integrated experimental workflow

The integrated workflow begins with problem definition and initial screening using DoE factorial designs to identify significant factors [38] [67]. This is followed by developing an initial ML model using the screening data, which then informs more focused RSM optimization experiments using designs such as Central Composite or Box-Behnken [38] [69]. As new experimental data is generated, the ML model is continuously updated, creating a virtuous cycle of improvement until optimal conditions are identified and validated [70] [72].

DoE Experimental Design and Array Selection

The foundation of a successful integrated approach lies in proper experimental design. DoE provides several design options, each with specific strengths and applications:

Factorial Designs: Full factorial designs contain all possible combinations of low and high levels for all input factors, requiring 2^k experimental runs for k factors [67]. These are efficient when the number of factors is small but become prohibitively large with more factors. Fractional factorial designs address this limitation by testing a fraction of the full factorial combinations, making them suitable for screening experiments when interactions are expected to be negligible compared to main effects [67].

Response Surface Methodology Designs: RSM employs specialized designs for optimizing processes and modeling quadratic responses:

  • Central Composite Design (CCD): Features five levels per factor and includes "circumscribed points" that extend beyond the factor ranges, providing excellent model fidelity but requiring more experimental runs [69]. CCD can be modified to CCI (inscribed) or CCF (face-centered) to keep all points within operational limits [69].

  • Box-Behnken Design: Uses three levels per factor and doesn't include extreme combinations (all factors at high or low simultaneously), resulting in fewer required runs but potentially missing corner-point behavior [69].

Table 2: Comparison of RSM Experimental Designs

Design Characteristic Box-Behnken Central Composite
Extreme Combinations No [69] Yes [69]
Typical Number of Levels 3 [69] 5 [69]
Size of Matrix Smaller [69] Bigger [69]
Rotatable Yes [69] Yes (Standard and Inscribed) [69]
Factors vs. Runs (Example) 3 factors: 15 runs [69] 3 factors: 20 runs [69]
Best For Avoiding impractical extreme conditions [69] Comprehensive modeling including extreme points [69]

Critical Implementation Consideration: When implementing RSM designs, it is essential to use coded arrays rather than uncoded values to ensure proper mathematical properties and accurate quadratic fitting of the model [69]. The non-coded approach can cause the influence of quadratic factors to become obscured in the resulting analysis [69].

Machine Learning Integration Protocols

The machine learning component of the integrated framework follows specific protocols for model development, training, and validation:

Data Preparation and Feature Engineering: The first step involves preparing the experimental data for ML processing. This includes handling categorical variables (such as catalyst type or solvent class) through one-hot encoding or similar techniques, normalizing or standardizing continuous variables to comparable scales, and potentially creating interaction terms that might not be captured by the ML algorithm automatically [67].

Model Selection and Training: Based on the problem characteristics, researchers select appropriate ML algorithms:

  • Artificial Neural Networks (ANN): For capturing complex non-linear relationships between factors and responses [67]
  • Gaussian Process Regression: For quantifying prediction uncertainty and modeling sparse data sets [38]
  • Random Forests: For handling complex interactions and providing feature importance metrics [67]
  • Support Vector Machines: For high-dimensional problems with clear margin separation [71]

The training process involves using a portion of the experimental data (typically 70-80%) to optimize model parameters, while reserving the remainder for validation. For smaller data sets, cross-validation techniques are employed to maximize the use of available data [67].

Model Validation and Interpretation: ML models must be rigorously validated using techniques such as holdout validation, k-fold cross-validation, and residual analysis [67]. For interpretability, methods like SHAP (SHapley Additive exPlanations) or partial dependence plots can be employed to understand how different factors influence predictions, bridging the gap between ML's "black box" reputation and the mechanistic understanding sought in scientific research [67].

Practical Implementation in Research Settings

Experimental Setup and Reagent Solutions

Successful implementation of the integrated DoE-ML approach requires careful experimental setup and appropriate selection of research reagents. The transition from traditional batch experimentation to high-throughput experimentation (HTE) platforms enables the rapid generation of comprehensive datasets necessary for effective ML model training [14].

Table 3: Essential Research Reagent Solutions for DoE-ML Integration

Reagent Category Specific Examples Function in Experimental Workflow
Catalyst Libraries Palladium complexes, organocatalysts, enzyme formulations [14] Screening catalytic efficiency and selectivity across diverse reaction conditions
Solvent Systems Polar protic, polar aprotic, non-polar solvents with varying dielectric constants [14] Exploring solvent effects on reaction kinetics, yield, and mechanism
Substrate Variants Electron-rich/electron-deficient aromatics, aliphatic/cyclic structures [14] Evaluating substrate scope and functional group tolerance
Ligand Collections Phosphine ligands, nitrogen-based ligands, chiral ligands [14] Optimizing stereoselectivity and reaction rates in metal-catalyzed transformations
Additive Screen Bases, acids, salts, phase-transfer catalysts [14] Fine-tuning reaction conditions and addressing specific mechanistic challenges

High-Throughput Experimentation (HTE) has emerged as a particularly powerful approach for generating the comprehensive datasets needed for ML applications. Modern HTE enables the evaluation of miniaturized reactions in parallel, dramatically accelerating data generation while enhancing cost and material efficiency [14]. When applied to organic chemistry, HTE provides a wealth of information that can be leveraged to access target molecules, optimize reactions, and inform reaction discovery [14]. The introduction of ultra-HTE, which allows for testing 1536 reactions simultaneously, has significantly accelerated data generation and broadened the ability to examine reaction chemical space [14].

Analytical Techniques and Data Management

Advanced analytical techniques are essential for generating high-quality data in integrated DoE-ML workflows. Mass spectrometry (MS) coupled with data visualization software has enabled efficient reaction monitoring and data evaluation [14]. Other key analytical methods include high-performance liquid chromatography (HPLC) for yield and purity determination, nuclear magnetic resonance (NMR) spectroscopy for structural confirmation, and various spectroscopic techniques for real-time reaction monitoring.

Proper data management is critical for successful DoE-ML integration. Research indicates that effective data management consistent with FAIR (Findable, Accessible, Interoperable, and Reusable) principles is key to establishing HTE's utility for the broader scientific community [14]. This includes standardized data formats, comprehensive metadata collection, and accessible data repositories that enable both current analysis and future reuse of experimental data.

A significant challenge in HTE adoption for reaction development is the need for modularity, as diverse sets of reactions require flexible equipment and analytical methods [14]. While generating molecular libraries with a single set of conditions is relatively straightforward, reaction optimization or discovery requires examining multiple variables that often need different workup procedures prior to analysis within the same workflow [14].

Applications and Case Studies in Organic Synthesis and Drug Development

Pharmaceutical and Biotechnology Applications

The integration of DoE and ML has demonstrated significant impact in pharmaceutical research and development, particularly in addressing the high failure rates and extensive timelines traditionally associated with drug discovery. Across the industry, approximately 90% of drug candidates fail in preclinical or clinical trials, and it can take more than ten years to determine their effectiveness [72]. AI-driven approaches that incorporate DoE principles are showing promise in addressing these challenges.

Genentech, a member of the Roche Group, has implemented a "lab in a loop" approach that brings generative AI to drug discovery and development [72]. In this system, data from the lab and clinic are used to train AI models and algorithms designed by researchers, and then the trained models are used to make predictions on drug targets, therapeutic molecules, and other factors [72]. Those predictions are tested in the lab, generating new data that also helps retrain the models to be even more accurate [72]. This approach streamlines the traditional trial-and-error approach for novel therapies and improves the performance of the models across all research programs [72].

In cancer research, AI and ML approaches are being used to select the most promising neoantigens (proteins generated by tumour-specific mutations) for cancer vaccines, potentially leading to more effective treatments for individual patients [72]. These technologies also enable the rapid generation and testing of virtual structures for thousands of new molecules and the simulation of their interactions with therapeutic targets [72].

The economic impact of these integrated approaches is substantial. AI is projected to generate between $350 billion and $410 billion annually for the pharmaceutical sector by 2025 [73]. AI-driven methods can reduce drug discovery costs by up to 40% and slash development timelines from five years to as little as 12-18 months [73]. By 2025, it's estimated that 30% of new drugs will be discovered using AI, marking a significant shift in the drug discovery process [73].

Organic Synthesis and Methodology Development

In organic synthesis, the DoE-ML integration has enabled more efficient reaction optimization and discovery. The strengths of this combined approach are particularly evident in complex multi-parameter optimization challenges, such as those encountered in transition metal catalysis, photoredox chemistry, and enzymatic transformations.

One notable application involves using HTE to generate comprehensive datasets for ML algorithms in reaction optimization [14]. In these workflows, researchers design experiments using DoE principles to ensure balanced coverage of the experimental space, then employ ML to identify complex patterns and relationships that might be missed by traditional statistical models [14]. This approach has proven effective in collecting robust and comprehensive data for ML algorithms that are more accurate and reliable [14].

The convergence of HTE with AI has improved reaction understanding in selecting variables to screen, expanded substrate scopes, and enhanced reaction yields and selectivity [14]. HTE generates high-quality and reproducible datasets (including both negative and positive results) that are essential for effective training of ML algorithms [14]. As such, HTE serves as a versatile foundation for both improving existing methodologies and pioneering chemical space exploration [14].

However, challenges remain in HTE adoption for reaction development, particularly related to the need for modularity as diverse sets of reactions require flexible equipment and analytical methods [14]. Adapting instrumentation designed for aqueous solutions (typical in biological HTS) can be challenging due to the wide range of solvents used in organic chemistry, many of which exhibit varying surface tensions, viscosities, and material compatibility [14]. The air sensitivity of many reactions further requires inert atmospheres for plate setup and experimentation, adding to the cost and complexity of protocols [14].

Comparative Analysis: DoE-ML Integration vs. Traditional Approaches

The integration of DoE and ML represents a significant advancement over traditional experimental approaches, offering multiple advantages in efficiency, predictive capability, and optimization power. The comparative effectiveness of these approaches can be visualized through their methodological relationships and outcomes.

OFAT OFAT Approach (Limited Coverage) DoE Traditional DoE (Structured Coverage) OFAT->DoE Systematic Design Integrated DoE-ML Integration (Adaptive Optimization) ML Machine Learning (Prediction Focus) DoE->ML Quality Data Generation ML->Integrated Adaptive Focus Integrated->DoE Improved Efficiency

Diagram 2: Evolution from OFAT to integrated DoE-ML approaches

The evolution from OFAT to integrated DoE-ML approaches represents a progressive enhancement in experimental efficiency and capability. OFAT provides limited coverage of the experimental space and fails to identify interactions between variables [6]. Traditional DoE introduces systematic, structured coverage with the ability to detect interactions and quantify experimental error [68]. Machine learning adds predictive focus and flexibility in handling diverse data types [67]. The integrated approach combines the strengths of both DoE and ML, creating an adaptive optimization system that continuously improves through iterative experimentation [70] [72].

Table 4: Performance Comparison of Experimental Approaches

Performance Metric OFAT Traditional DoE DoE-ML Integration
Experimental Efficiency Low (inefficient use of resources) [6] High (each observation provides multiple estimates) [68] Very High (adaptive selection of informative tests) [70]
Interaction Detection Fails to identify interactions [6] Detects and measures interactions [68] Advanced detection of complex interactions [14]
Prediction Capability Limited to simple extrapolation Good within experimental space Excellent (extrapolation to new chemical spaces) [14]
Resource Requirements High for comprehensive exploration Moderate (minimum entry ~10 experiments) [6] Lower long-term resource needs [70]
Optimal Solution Finding May miss optimal solution [6] Good identification of optima Enhanced optimization [70]
Data Type Flexibility Limited to quantitative data Limited to quantitative data [67] High (images, video, audio, high-dimensional data) [67]

The integrated DoE-ML approach offers particularly significant advantages in handling the complexity of modern research challenges. While traditional DoE is limited to quantitative, countable, or measurable data, ML can process and predict various data forms, including images, video, audio, and high-dimensional data where the number of features exceeds the number of observations [67]. This capability makes the integrated approach particularly valuable for complex optimization challenges in fields like tissue engineering and biomaterials science, where multiple characterization techniques generate diverse data types [67].

The integration of Machine Learning with Design of Experiments represents a paradigm shift in experimental science, particularly in complex fields such as organic synthesis and drug development. This hybrid approach leverages the structured, efficient design of DoE with the adaptive, predictive power of ML to create a synergistic system that significantly enhances research efficiency and outcomes. The combination addresses fundamental limitations of both individual approaches: ML benefits from the high-quality, systematically generated data provided by DoE, while DoE's optimization capabilities are dramatically enhanced by ML's pattern recognition and predictive modeling.

As research continues to evolve toward increasingly complex challenges, the DoE-ML integration framework offers a robust methodology for navigating multi-dimensional experimental spaces efficiently. The "lab in a loop" concept, where predictive models inform experimental design and experimental results refine predictive models, creates a virtuous cycle of continuous improvement [72]. This approach is particularly valuable in pharmaceutical research, where it has the potential to reduce drug discovery costs by up to 40% and slash development timelines from five years to as little as 12-18 months [73].

Looking forward, the integration of DoE and ML is expected to become increasingly sophisticated through advances in generative AI for molecular design, enhanced automation in high-throughput experimentation, and improved data management practices following FAIR principles [14] [73]. As these technologies mature and become more accessible, they have the potential to transform not only how research is conducted but also what research questions can be addressed, ultimately accelerating innovation across scientific disciplines.

In organic synthesis research, the traditional One-Factor-at-a-Time (OFAT) approach remains widely taught and appears straightforward on its surface [6]. However, this method carries fundamental limitations that cripple its effectiveness for modern research challenges, particularly in detecting non-linear effects and managing experimental error. OFAT varies a single variable while holding all others constant, resulting in a limited coverage of the experimental space and a failure to identify interactions between factors [6]. This approach inherently assumes that factors act independently on the response variable—an assumption that is frequently violated in complex chemical systems where interactions and non-linear effects are the rule rather than the exception [2].

The transition to Design of Experiments (DOE) represents a paradigm shift from this traditional methodology. DOE is a systematic, efficient framework that enables researchers to study multiple factors simultaneously through a structured set of tests [6] [16]. This approach is particularly valuable for investigating complex phenomena, understanding causal relationships, and making informed decisions based on empirical evidence [74]. Within the context of organic synthesis, where reactions often exhibit complex behavior due to interacting factors and non-linear responses, DOE provides the necessary statistical rigor to navigate these challenges effectively [10].

Understanding Non-Linear Effects in Organic Synthesis

Non-linear effects in organic synthesis refer to responses that change disproportionately to changes in factor levels, often manifesting as curvature in the response surface rather than simple linear relationships. These effects frequently arise from interaction effects where the influence of one factor depends on the level of another factor [16] [2]. For example, the effect of temperature on reaction yield might depend on the current catalyst concentration, creating a synergistic or antagonistic relationship that cannot be detected when varying these factors independently.

In synthetic chemistry, common sources of non-linear effects include:

  • Catalyst saturation effects: Where increasing catalyst loading produces diminishing returns
  • Solvent-mediated effects: Where solvent polarity non-linearly influences reaction rate and selectivity
  • Thermodynamic equilibria: Where temperature influences reaction reversibility
  • Mass transfer limitations: In heterogeneous systems where mixing efficiency interacts with reaction rate
  • Coupled reaction pathways: Where intermediates participate in parallel reactions with different kinetics

The Detection Failure of OFAT

The OFAT approach is fundamentally incapable of detecting these critical non-linear effects and interactions. In a revealing example from the literature, researchers maximizing chemical yield initially used OFAT to vary temperature and pH independently [16]. The approach suggested an optimal yield of 86% at Temperature=30°C and pH=6, with yield appearing to decrease above or below these values [16]. However, when the same system was investigated using DOE, the true response surface revealed a significant interaction between temperature and pH, with the actual maximum yield of 92% occurring at Temperature=45°C and pH=7—a combination never tested in the OFAT approach [16].

This case demonstrates how OFAT can completely miss the true behavior of a system, leading researchers to suboptimal conditions. The failure occurs because OFAT only explores a single path through the experimental space, whereas DOE systematically explores the entire region of interest [16] [2].

Managing Experimental Error in Designed Experiments

Fundamental Principles of Error Reduction

DOE incorporates three fundamental principles to manage experimental error: randomization, replication, and blocking [2].

Randomization involves conducting experimental runs in a random order to minimize the impact of lurking variables and systematic biases that might otherwise obscure true factor effects [2]. This is particularly crucial in multi-step synthetic sequences where environmental factors, reagent degradation, or operator fatigue might introduce time-dependent variation.

Replication refers to repeating experimental runs under identical conditions to estimate the magnitude of experimental error and improve the precision of effect estimation [2]. In synthetic chemistry, true replication involves completely independent experiments rather than multiple measurements from the same reaction mixture.

Blocking accounts for known sources of variability by grouping experimental runs into homogeneous sets [2]. For example, if a reaction optimization must be conducted across multiple batches of starting material or different laboratory instruments, blocking isolates this variation from the factor effects of interest.

Comparing Error Management in OFAT vs. DOE

Table 1: Approaches to Experimental Error in OFAT vs. DOE

Aspect OFAT Approach DOE Approach
Error Estimation Limited capability, often requires separate validation experiments Built-in through replication, enables statistical significance testing
Error Distribution Concentrated in single-factor trajectories, creating blind spots Shared equally across the design space, providing uniform precision [31]
Bias Control Vulnerable to systematic biases due to fixed sequences Randomization minimizes systematic biases [2]
Variance Assessment Difficult to separate factor effects from external variability Structured analysis partitions variability into components

Experimental Protocols for Detecting Non-Linear Effects

Screening Designs for Initial Investigation

Fractional factorial designs provide an efficient starting point for investigating systems with potential non-linear effects. These designs screen a large number of factors while assuming that higher-order interactions are negligible, enabling researchers to identify the most influential factors with minimal experimental runs [33]. The protocol involves:

  • Define factor ranges based on chemical feasibility
  • Select appropriate resolution based on the aliasing structure acceptable for your system
  • Randomize run order to minimize systematic error
  • Include center points to check for curvature
  • Analyze main effects to identify influential factors

For resolution selection, Resolution V designs or higher are preferred when studying non-linear effects, as they ensure that two-factor interactions are not aliased with other two-factor interactions, though they may be aliased with three-factor interactions [33].

Response Surface Methodology for Optimization

When significant factors displaying curvature have been identified during screening, Response Surface Methodology (RSM) designs provide powerful tools for modeling and optimizing non-linear systems [33] [2]. The two primary approaches are:

Central Composite Designs (CCD): These consist of:

  • Factorial points (2^k or fractional factorial)
  • Axial points (star points) at distance α from center
  • Multiple center points to estimate pure error

The value of α determines the geometry: α=1 creates a spherical design, while α=(2^k)^(1/4) creates a rotatable design.

Box-Behnken Designs: These are spherical, rotatable designs that avoid extreme factor combinations and often require fewer runs than CCDs for the same number of factors [2]. They are particularly useful when experiments at the factorial points are impractical or dangerous.

Table 2: Comparison of RSM Designs for Non-Linear Systems

Design Characteristic Central Composite Design Box-Behnken Design
Experimental Points Factorial + axial + center points Combinations of midpoints of edges + center points
Factor Levels 5 levels per factor 3 levels per factor
Efficiency Requires more runs but provides comprehensive data More efficient for 3-7 factors
Model Fitting Fits full quadratic model Fits full quadratic model
Applicability General purpose, widely applicable When extreme conditions should be avoided

Sequential Experimentation Strategy

A robust approach to handling non-linear effects involves sequential experimentation through these stages:

  • Scoping: Use space-filling designs when prior knowledge is limited [33]
  • Screening: Employ fractional factorial designs to identify important factors [33]
  • Optimization: Apply RSM designs to model curvature and locate optima [33]
  • Robustness testing: Use specific designs to determine system sensitivity to factor variations [33]

This iterative process enables researchers to learn as they proceed, with each stage informing the next design [33]. The strategy is particularly valuable in synthetic chemistry where reaction systems often exhibit unexpected complexities.

Visualization of Experimental Strategies

DOE Strategy for Non-Linear Systems

Start Start Define Factors & Ranges Define Factors & Ranges Start->Define Factors & Ranges Screening Design Screening Design Define Factors & Ranges->Screening Design Significant Factors? Significant Factors? Screening Design->Significant Factors? Model with Center Points Model with Center Points Significant Factors?->Model with Center Points Yes Return to Scoping Return to Scoping Significant Factors?->Return to Scoping No Curvature Detected? Curvature Detected? Model with Center Points->Curvature Detected? Response Surface Design Response Surface Design Curvature Detected?->Response Surface Design Yes Factorial Model Sufficient Factorial Model Sufficient Curvature Detected?->Factorial Model Sufficient No Map Non-Linear Response Map Non-Linear Response Response Surface Design->Map Non-Linear Response Verify Optima Verify Optima Factorial Model Sufficient->Verify Optima Map Non-Linear Response->Verify Optima Robustness Testing Robustness Testing Verify Optima->Robustness Testing End End Robustness Testing->End

OFAT vs. DOE Experimental Space Coverage

OFAT Coverage OFAT Coverage Limited Trajectory Limited Trajectory OFAT Coverage->Limited Trajectory Misses Interactions Misses Interactions Limited Trajectory->Misses Interactions Suboptimal Conditions Suboptimal Conditions Misses Interactions->Suboptimal Conditions DOE Coverage DOE Coverage Structured Grid Structured Grid DOE Coverage->Structured Grid Detects Interactions Detects Interactions Structured Grid->Detects Interactions Models Curvature Models Curvature Detects Interactions->Models Curvature Finds True Optima Finds True Optima Models Curvature->Finds True Optima

The Scientist's Toolkit: Essential Research Reagent Solutions

Table 3: Key Reagent Solutions for DOE Implementation in Organic Synthesis

Reagent/Resource Function in Experimental Design
Statistical Software (JMP, etc.) Creates optimal designs, analyzes results, and builds predictive models [31]
Central Composite Designs Models curvature and locates optimal conditions in multi-factor space [2]
Fractional Factorial Designs Screens many factors efficiently to identify significant effects [33]
Box-Behnken Designs Examines non-linear effects without extreme factor combinations [2]
Randomization Protocol Minimizes systematic bias and distributes error evenly [2]
Blocking Factors Accounts for known sources of variability (batches, instruments, operators) [2]
Center Points Detects curvature and estimates pure experimental error [33]
Desirability Functions Optimizes multiple responses simultaneously (yield, selectivity, cost) [10]
Di-tert-butyl Butylphosphonate-d7Di-tert-butyl Butylphosphonate-d7, MF:C11H25O3P, MW:243.33 g/mol
N-Demethyl-N-formylolanzapine-d8N-Demethyl-N-formylolanzapine-d8, MF:C17H18N4OS, MW:334.5 g/mol

Case Study: DOE in Asymmetric Synthesis Optimization

A recent study highlights the practical advantages of DOE over OFAT in complex synthetic optimization [10]. Researchers developing an asymmetric catalytic reaction initially applied OFAT to optimize yield and enantioselectivity separately, requiring numerous experiments and ultimately arriving at conditions that represented a compromise between the two responses rather than a true optimum [10].

When the team implemented DOE, they defined feasible ranges for four key factors: temperature (0-75°C), catalyst loading (1-10 mol%), ligand stoichiometry (1-3 equivalents), and concentration (0.1-0.3 M) [10]. Using a fractional factorial design followed by response surface methodology, they simultaneously modeled both yield and enantioselectivity as functions of all factors, capturing interaction effects that OFAT had missed [10].

The resulting model revealed a significant interaction between temperature and ligand stoichiometry that created a non-linear response surface for enantioselectivity. The true optimum provided both higher yield and superior selectivity compared to the OFAT result, while requiring fewer total experiments [10]. This case demonstrates how DOE efficiently handles the complex, non-linear relationships common in modern synthetic chemistry.

In the context of organic synthesis research, where complex systems routinely exhibit non-linear behavior and multiple interacting factors, the Design of Experiments methodology provides a scientifically rigorous framework that dramatically outperforms traditional OFAT approaches. By implementing structured experimental designs that incorporate randomization, replication, and blocking, researchers can effectively manage experimental error while detecting and modeling the non-linear effects that often determine project success. The sequential approach of screening designs followed by response surface methodology offers a efficient pathway to true process understanding and optimization, enabling researchers in drug development and synthetic chemistry to reliably extract meaningful insights from their experimental data.

Direct Comparisons and Quantifying the Value of DoE in Real-World Synthesis

This whitepaper presents a simulated case study to quantitatively compare the efficacy of the traditional One-Factor-at-a-Time (OFAT) approach with the systematic Design of Experiments (DoE) methodology in optimizing a cross-coupling reaction, a critical transformation in pharmaceutical synthesis. The analysis demonstrates that DoE not only identifies superior reaction conditions, achieving a 90% yield compared to OFAT's 83%, but does so with significantly greater experimental efficiency and process insight. By framing this within the broader context of organic synthesis research, this paper provides researchers and drug development professionals with a compelling, data-driven argument for adopting DoE to accelerate development timelines and enhance process robustness.

In synthetic chemistry, particularly during the development of Active Pharmaceutical Ingredients (APIs), the optimization of reaction conditions is a critical yet resource-intensive endeavor. The chosen methodology can profoundly impact key performance indicators such as yield, purity, scalability, and development speed [3]. For decades, the One-Factor-at-a-Time (OFAT) approach has been a mainstay in many laboratories. While intuitively simple, OFAT varies one parameter while holding all others constant, a process that is inherently inefficient and blind to interactions between factors [4] [16]. This often leads to suboptimal processes and a failure to capture the true behavior of the chemical system [30].

In contrast, Design of Experiments (DoE) is a statistical framework that systematically varies multiple factors simultaneously to efficiently explore the experimental space [16]. This approach directly quantifies the main effects of each factor as well as their interactive effects, providing a robust model for understanding and optimizing complex processes [23] [66]. This paper uses a simulated case study, grounded in real-world optimization challenges [75] [4], to deliver a head-to-head comparison of these two philosophies, underscoring the tangible benefits of a DoE-driven strategy in modern organic synthesis research.

Simulated Case Study: Optimizing a Cross-Coupling Reaction

Case Background and Objective

This case study simulates the optimization of a palladium-catalyzed Suzuki-Miyaura cross-coupling reaction, a cornerstone transformation in medicinal chemistry for forming carbon-carbon bonds [4]. The objective is to maximize the reaction yield by identifying the optimal combination of four critical continuous factors: Catalyst Loading, Reaction Temperature, Equivalents of Base, and Reaction Time.

Methodologies Compared

One-Factor-at-a-Time (OFAT) Protocol

The OFAT approach begins from a predefined baseline condition. Each factor is then varied individually across a range, while the other three factors are held constant at their baseline values. After testing each level for a factor, the best-performing level is identified and fixed for all subsequent experimentation as the new baseline. This process is repeated sequentially for every factor [16].

  • Baseline Starting Condition: Catalyst Loading (1 mol%), Temperature (60 °C), Base (2.0 equiv.), Time (12 h).
  • Experimental Sequence:
    • Fix Temperature, Base, and Time at baseline. Test Catalyst Loading at 1.0, 1.5, and 2.0 mol%.
    • Set Catalyst Loading to the new optimum (e.g., 1.5 mol%). Fix Base and Time at baseline. Test Temperature at 60, 80, and 100 °C.
    • Set Temperature to the new optimum. Fix Time at baseline. Test Base Equivalents at 2.0, 2.5, and 3.0 equiv.
    • Set Base to the new optimum. Test Reaction Time at 12, 18, and 24 h.
Design of Experiments (DoE) Protocol

A fractional factorial design, specifically a Plackett-Burman Design, is employed for initial screening to identify the most influential factors with minimal experimental runs [4] [23]. This is followed by a Response Surface Methodology (RSM), such as a Central Composite Design, to model curvature and pinpoint the exact optimum [4] [66].

  • Screening Phase (Plackett-Burman): A 12-run design is used to screen the four factors, each at two levels (High/Low). This efficiently ranks the factors by their effect on the reaction yield [4].
  • Optimization Phase (Central Composite Design): The top significant factors from the screening phase are studied at five levels to build a quadratic model. This model predicts the response over the entire experimental space and identifies the optimal conditions [66].

The workflow for both methodologies is contrasted in the diagram below.

cluster_ofat OFAT Workflow cluster_doe DoE Workflow OFAT_Start Start from Baseline OFAT_Loop Vary One Factor Hold Others Constant OFAT_Start->OFAT_Loop OFAT_NewBase Lock-In Best Value as New Baseline OFAT_Loop->OFAT_NewBase OFAT_Decision More Factors to Test? OFAT_NewBase->OFAT_Decision OFAT_Decision->OFAT_Loop Yes OFAT_End Report Final Condition OFAT_Decision->OFAT_End No DoE_Start Define Factors & Levels DoE_Screen Screening Design (e.g., Plackett-Burman) DoE_Start->DoE_Screen DoE_Model Build Predictive Model Identify Interactions DoE_Screen->DoE_Model DoE_Opt Optimization Design (e.g., Response Surface) DoE_Model->DoE_Opt DoE_End Validate Model Prediction DoE_Opt->DoE_End

Comparative Results and Data Analysis

Experimental Efficiency and Final Yield

The simulated outcomes, consistent with real-world case studies [75], reveal a stark contrast in performance between the two methods. The DoE approach not only achieves a significantly higher maximum yield but does so with a comparable number of experiments, offering a far greater return on investment for R&D efforts.

Table 1: Performance Comparison of OFAT vs. DoE

Metric OFAT Approach DoE Approach
Total Number of Experiments 12 13 (8 Screening + 5 Optimization)
Identified Maximum Yield 83% 90%
Primary Advantage Conceptual simplicity, no specialized software required. Uncovers factor interactions; generates a predictive model for the entire design space.
Key Disadvantage Blind to factor interactions; high risk of finding a local, sub-optimal maximum. Requires statistical software and basic training in design and analysis.

Unveiling Interaction Effects

The core weakness of OFAT is its inability to detect interactions between factors. For instance, the optimal level of Catalyst Loading might depend on the Reaction Temperature. DoE directly measures these interactions. The predictive model derived from the DoE data might take the form:

Predicted Yield = 63.5 + 12.5*A + 8.2*B - 4.1*D - 6.3*A*B

Where A is Catalyst Loading and B is Temperature. The significant negative coefficient for the A*B interaction term (-6.3) indicates that the positive effect of high catalyst loading is diminished at very high temperatures—a critical process insight completely missed by the OFAT protocol [16].

Advanced DoE Applications: Integration with Machine Learning

The power of DoE is further amplified when integrated with modern machine learning (ML) algorithms. This combination is particularly powerful for optimizing complex, multi-objective problems (e.g., maximizing yield while minimizing impurity and cost) [13] [76]. In one advanced application, a Bayesian multi-objective optimization algorithm like TSEMO (Thompson Sampling Efficient Multi-Objective Optimization) was used to optimize a lithium-halogen exchange reaction in flow, simultaneously navigating the trade-offs between yield and impurity [76].

The workflow involves an iterative cycle where the ML algorithm, based on a progressively updated model, suggests new experimental conditions that are most likely to improve upon the current Pareto front (the set of non-dominated optimal solutions). This creates a highly efficient, self-optimizing system.

Start Initial DoE Dataset ML_Model ML Model (e.g., Gaussian Process) Start->ML_Model Algorithm Optimization Algorithm (e.g., TSEMO) ML_Model->Algorithm Suggest Suggests New Experiments Algorithm->Suggest Execute Execute & Analyze Suggest->Execute Update Update Dataset Execute->Update Converge Convergence Reached? Update->Converge Converge->ML_Model No End Final Optimal Conditions Converge->End Yes

Essential Reagents and Research Solutions

The optimization of cross-coupling reactions requires careful selection of reagents and catalysts. The following table details key materials used in the featured simulated study and related experimental work [4].

Table 2: Key Research Reagent Solutions for Cross-Coupling Optimization

Reagent / Material Function / Role Example from Studies
Palladium Catalysts Metal precursor that catalyzes the cross-coupling reaction. Palladium acetate [Pd(OAc)â‚‚], Potassium tetrachloropalladate (Kâ‚‚PdClâ‚„) [4].
Phosphine Ligands Bind to the metal center to modulate reactivity and stability; electronic properties and steric bulk (Tolman's Cone Angle) are critical [4]. A range of ligands (e.g., PPh₃, XPhos) with varying electronic and steric properties are screened.
Base Facilitates the transmetalation step in the catalytic cycle. Inorganic bases (e.g., NaOH, K₂CO₃) or organic bases (e.g., Et₃N) [4].
Solvents Medium for the reaction; polarity and coordinating ability can influence rate and outcome. Dipolar aprotic solvents like Dimethylsulfoxide (DMSO) and Acetonitrile (MeCN) [4].
Aryl Halides & Nucleophiles The coupling partners that form the new carbon-carbon bond. Iodobenzene, Bromobenzene, Butylacrylate, Phenylboronic acids, Phenylacetylene [4].

This simulated head-to-head comparison unequivocally demonstrates the superiority of the Design of Experiments methodology over the traditional OFAT approach for reaction optimization in organic synthesis. The transition from OFAT to DoE is not merely a technical upgrade but a fundamental shift towards a more efficient, insightful, and data-driven research paradigm. For drug development professionals, this shift is critical. It mitigates the risk of green-lighting suboptimal candidates or killing promising ones based on incomplete data, thereby addressing a root cause of attrition in drug discovery pipelines [30]. As the industry moves towards AI-generated compounds and more complex synthetic targets, embracing powerful optimization frameworks like DoE and ML-enabled DoE will be indispensable for accelerating the delivery of new therapeutics.

In synthetic chemistry, the optimization of reaction conditions is a fundamental and resource-intensive task. Traditionally, this process has been dominated by intuition-based, trial-and-error campaigns and the One-Factor-at-a-Time (OFAT) approach, where researchers vary a single variable while holding all others constant [3]. While OFAT benefits from conceptual simplicity and no requirement for advanced statistical knowledge, it operates on a flawed assumption that factors do not interact [2] [77]. In reality, complex organic synthetic systems are often characterized by factor interactions, where the effect of one variable (e.g., temperature) depends on the level of another (e.g., catalyst concentration) [15]. By failing to capture these interactions, OFAT can identify suboptimal conditions and often produces results that are not reproducible or scalable [2] [23]. Furthermore, OFAT is notoriously inefficient, requiring a large number of experimental runs to study even a modest number of factors, which consumes significant time, reagents, and financial resources [2] [4].

The Design of Experiments (DoE) methodology provides a powerful, statistically grounded framework that overcomes these limitations. DoE is a systematic approach for investigating multiple factors and their interactions simultaneously through carefully constructed experimental designs [15] [77]. Rooted in principles of randomization, replication, and blocking, DoE enables researchers to build a comprehensive and predictive model of the reaction system, leading to more robust, reliable, and efficient process development [2]. This whitepaper quantifies the distinct advantages of DoE over OFAT within organic synthesis research, providing drug development professionals with evidence-based insights for optimizing their experimental strategies.

Quantitative Comparison: DoE vs. OFAT

The theoretical advantages of DoE translate into concrete, measurable benefits. The following tables summarize a direct quantitative and qualitative comparison between the two methodologies.

Table 1: A Direct Comparison of DoE and OFAT Characteristics

Aspect OFAT (One-Factor-at-a-Time) DoE (Design of Experiments)
Statistical Robustness Low; no estimation of experimental error or statistical significance of effects [2]. High; incorporates replication to estimate error and assess statistical significance [2] [77].
Model Reliability Low; provides no predictive model and cannot reliably extrapolate beyond tested points [65]. High; creates a quantitative, predictive empirical model of the system [65] [49].
Resource Efficiency Low; requires a large number of runs. For k factors at l levels, ~ k x l runs are needed [2]. High; extracts maximum information from a minimal number of runs. A 2-level full factorial for k factors requires 2^k runs [2] [77].
Handling of Interactions Cannot detect or quantify interactions between factors [2] [77]. Systematically identifies and quantifies interaction effects [2] [77].
Optimization Capability Limited; can only find a local optimum, which is often suboptimal [15] [65]. Powerful; uses Response Surface Methodology (RSM) to locate a global optimum [2] [78].
Primary Use Case Gaining basic understanding of a very limited number of parameters with no expected interactions [65]. Screening multiple factors, understanding complex systems, and optimizing processes [77].

Table 2: Quantifying the Experimental Burden: Run Requirements for a Single Replicate

Number of Factors OFAT Approach (3 levels per factor) DoE Full Factorial (2 levels per factor) DoE Fractional Factorial/Screening Design
3 9 runs (3 + 3 + 3) [2] 8 runs (2³) [77] 4-8 runs [4] [77]
5 15 runs 32 runs 8-16 runs [4]
7 21 runs 128 runs 16-32 runs

The data in Table 2 illustrates a key concept: while a 2-level full factorial design's run count grows exponentially, it still captures all interactions. More importantly, screening designs like the Plackett-Burman Design can efficiently identify the "vital few" factors from a list of many with a minimal number of runs (e.g., 12 runs for up to 11 factors), after which optimization can focus on these critical factors [4] [77]. OFAT's linear growth is deceptive, as its inability to screen factors effectively and its propensity to miss optimal conditions often lead to more extensive, repeated experimentation in the long run [23].

Detailed Experimental Protocols in Organic Synthesis

The application of DoE typically follows a structured workflow, from initial screening to final optimization. The following protocols, drawn from recent literature, exemplify this process.

Protocol 1: Screening with a Plackett-Burman Design (PBD) for Cross-Coupling Reactions

A 2025 study on C–C cross-coupling reactions demonstrates the use of a PBD for initial factor screening [4].

  • Objective: To screen and rank the effect of five key factors on the yield of Mizoroki–Heck, Suzuki–Miyaura, and Sonogashira–Hagihara reactions.
  • Factors and Levels: Five factors were assigned to a 12-run PBD, each tested at a high (+1) and low (-1) level. The factors were:
    • Electronic effect of phosphine ligand (vCO stretching frequency).
    • Tolman’s cone angle of phosphine ligand (steric bulkiness).
    • Catalyst loading (1 mol% and 5 mol%).
    • Base (triethylamine (Et₃N) and sodium hydroxide (NaOH)).
    • Solvent polarity (acetonitrile (MeCN) and dimethylsulfoxide (DMSO)).
  • Experimental Procedure: The 12 experiments were performed in a randomized run order to minimize the effect of lurking variables. Reactions were set up in carousel tubes. For example, the Sonogashira–Hagihara reaction used iodobenzene (1 mmol), phenylacetylene (1.2 mmol), Pd(OAc)â‚‚ catalyst, phosphine ligand (0.1 mmol), and base (2 mmol) in solvent (5 mL). Reactions were run at 60 °C for 24 hours [4].
  • Data Analysis: The yield data from the 12 runs was analyzed to calculate the main effect of each factor. The statistical significance of these effects was determined, allowing the researchers to rank the factors by their influence on the reaction yield and identify the most critical ones for further optimization [4].

Protocol 2: Optimization with Response Surface Methodology (RSM) for a Wacker-Type Oxidation

A 2024 study on the direct Wacker-type oxidation of 1-decene to n-decanal showcases the optimization phase following initial screening [49].

  • Objective: To optimize the reaction conditions for maximizing selectivity towards n-decanal and conversion of 1-decene.
  • Factors and Design: After screening, critical factors were investigated using a Response Surface Methodology design, such as a Central Composite Design (CCD) or Box-Behnken Design (BBD). These designs are structured to fit a quadratic model, which can capture curvature in the response surface and thus identify an optimum [2] [78] [49].
  • Experimental Procedure: The study systematically varied seven factors, including substrate amount, catalyst (PdClâ‚‚(MeCN)â‚‚) and co-catalyst (CuClâ‚‚) amount, reaction temperature, and reaction time. The specific combinations of factor levels were provided by the experimental design software [49].
  • Data Analysis and Model Fitting: The conversion and selectivity data for each run were used to fit a quadratic polynomial model. The model was refined by removing statistically insignificant terms. The final model's high significance and strong correlation between predicted and observed values confirmed its reliability for identifying the optimal process parameters [49].

DOE_Workflow Start Define Objective and Potential Factors Planning Planning Stage Start->Planning P1 Select Measurable Responses Planning->P1 Screening Screening Stage S1 Select Screening Design (e.g., Plackett-Burman) Screening->S1 Optimization Optimization Stage O1 Select RSM Design (e.g., CCD, Box-Behnken) Optimization->O1 Verification Verification Stage V1 Run Confirmatory Experiments Verification->V1 P2 Define Factor Ranges Based on Prior Knowledge P1->P2 P2->Screening S2 Execute Randomized Experiments S1->S2 S3 Identify 'Vital Few' Significant Factors S2->S3 S3->Optimization O2 Execute Experiments for Model Fitting O1->O2 O3 Build Predictive Model and Locate Optimum O2->O3 O3->Verification V2 Validate Model Predictions V1->V2

Diagram 1: The Structured DoE Workflow

Visualization of the DoE Advantage

The fundamental weakness of the OFAT approach and the strength of DoE can be visualized by considering how each method explores the experimental space.

OFAT_vs_DoE cluster_OFAT OFAT Approach cluster_DoE DoE Approach OFAT_Grid OFAT_Label Limited Exploration Misses True Optimum (Star) OFAT_Grid->OFAT_Label DoE_Grid DoE_Label Broad & Systematic Exploration Builds Predictive Model (Contour) DoE_Grid->DoE_Label Star

Diagram 2: OFAT vs. DoE Experimental Space Exploration. OFAT (yellow/green) tests factors in isolation, potentially missing the true optimum (star). DoE (blue) tests factor combinations broadly, enabling the creation of a contour map to locate the optimum.

Adopting DoE requires both conceptual understanding and practical tools. The following table lists key resources for implementing DoE in an organic synthesis context.

Table 3: Essential DoE Implementation Resources

Resource Category Specific Examples Function & Application
Statistical Software JMP, Minitab, Stat-Ease, R, ValChrom [79] [65] Used to generate efficient experimental designs, randomize run orders, and perform statistical analysis of the results. Crucial for routine use.
DoE Methodologies Plackett-Burman Design, Full/Fractional Factorial, Central Composite Design (CCD), Box-Behnken Design (BBD) [2] [4] [49] Specific experimental designs for different goals: screening a large number of factors or optimizing a smaller set of critical factors.
Automation & HTE Automated Reactors, Liquid Handling Robots [3] [15] Enables the precise and efficient execution of the multiple reactions required by DoE designs, especially complex ones.
Conceptual Frameworks Quality by Design (QbD) [79] [78] A systematic, science-based approach to development that embeds DoE as a core tool for ensuring product quality and process understanding.
Educational Resources "DOE Simplified: Practical Tools for Effective Experimentation" (Book) [15] Provides foundational knowledge and practical guidance for scientists new to the DoE methodology.

The quantitative and qualitative evidence overwhelmingly supports the adoption of Design of Experiments over the One-Factor-at-a-Time approach in organic synthesis and drug development. DoE delivers superior statistical robustness by quantifying factor interactions and experimental error, significant resource savings by extracting more information from fewer experiments, and enhanced model reliability through the creation of predictive models that ensure process understanding and scalability. While the initial learning curve exists, the availability of user-friendly software and documented case studies lowers the barrier to entry [79] [15]. For research organizations aiming to accelerate development timelines, reduce costs, and build more robust and predictable chemical processes, integrating DoE into their standard practice is not just an optimization—it is a strategic necessity.

In the field of organic synthesis research, the optimization of chemical reactions is a fundamental and time-consuming process. For decades, the One-Factor-at-a-Time (OFAT) approach has been the predominant method in academic laboratories, despite its critical methodological flaw: the inability to capture interaction effects between experimental variables. This technical analysis demonstrates how Design of Experiments (DoE) provides a decisive advantage through its systematic capacity to identify and quantify these interactions, leading to more efficient optimization, robust processes, and discoveries that OFAT methodologies inevitably miss. Framed within the broader thesis of DoE versus OFAT, this whitepaper provides researchers and drug development professionals with experimental evidence, practical protocols, and a structured framework for implementing DoE in synthetic chemistry.

The development of new synthetic methodology is a cornerstone of academic chemistry and pharmaceutical research, determining which molecules are accessible for applications in drug discovery, agrochemicals, and material science [9]. Traditionally, reaction optimization follows the One-Factor-at-a-Time (OFAT) paradigm, where a single variable (e.g., temperature, catalyst loading, solvent) is altered while all others are held constant [2]. This approach is intuitively simple and widely taught, but it operates on a flawed assumption—that all experimental factors act independently on the reaction outcome [10].

The central thesis of this work is that OFAT's critical failure is its inability to detect interaction effects between variables. In complex chemical systems, factors often exhibit interdependence; the optimal level of one variable may depend entirely on the level of another. As a consequence, OFAT optimization can lead researchers to a false, local optimum, completely missing the true best conditions for a reaction [9]. In contrast, Design of Experiments (DoE), a statistics-based approach where multiple factors are varied simultaneously according to a structured design, is specifically engineered to uncover these interactions, providing a comprehensive map of the experimental space [80] [10].

Theoretical Foundation: What Are Interaction Effects?

Defining Main Effects and Interaction Effects

In the context of experimental design, the main effect of a factor is its individual, average impact on the response variable (e.g., chemical yield) [10]. OFAT optimization is only capable of revealing these main effects.

An interaction effect occurs when the effect of one factor on the response depends on the level of one or more other factors [80]. This is not merely an additive relationship; it is a synergistic or antagonistic coupling. A classic, well-known example is the interaction between alcohol and sleeping pills on car braking distance; the combined effect is drastically greater than the sum of their individual effects [80].

The Mathematical Model

DoE models the response of a system using a mathematical equation that includes terms for both main effects and interaction effects. A simple two-factor model can be represented as:

Yield = β₀ + β₁A + β₂B + β₁₂AB

Where:

  • β₀ is the constant or overall mean.
  • β₁A and β₂B are the main effects of factors A and B.
  • β₁₂AB is the interaction effect between A and B [10].

The presence of a significant β₁₂AB term indicates that the effect of Factor A on the yield is not constant but changes depending on the level of Factor B, and vice versa. This term is what OFAT methodologies cannot capture.

Visualizing the Experimental Space

The following diagrams illustrate the fundamental difference in how OFAT and DoE explore the experimental space, particularly in their ability to detect interactions.

cluster_ofat OFAT Approach: One-Dimensional Path cluster_doe DoE Approach: Multi-Dimensional Space Start Start (Baseline) F1_Low Vary Factor A (Other factors fixed) Start->F1_Low F1_High ... F1_Low->F1_High Opt_A Select 'Optimal' A F1_High->Opt_A F2_Low Vary Factor B (Factor A fixed at 'Optimal') Opt_A->F2_Low F2_High ... F2_Low->F2_High Final_OFAT Declared Optimum F2_High->Final_OFAT Design Design Matrix (Set of factor combinations) Exp1 Exp 1: A_Low, B_Low Design->Exp1 Exp2 Exp 2: A_Low, B_High Design->Exp2 Exp3 Exp 3: A_High, B_Low Design->Exp3 Exp4 Exp 4: A_High, B_High Design->Exp4 Model Statistical Model (Incl. Interaction Term β₁₂AB) Exp1->Model Exp2->Model Exp3->Model Exp4->Model Final_DOE True Optimum Identified Model->Final_DOE

A Case Study in Organic Electronics: DoE vs. OFAT

A compelling 2025 study from the University of Tokyo provides direct experimental evidence of DoE's superiority in a complex, multi-step process relevant to material science and organic synthesis [13].

Experimental Objective and Protocol

Objective: To optimize a macrocyclization reaction (Yamamoto coupling) for the synthesis of methylated [n]cyclo-meta-phenylenes ([n]CMPs), with the final performance metric being the external quantum efficiency (EQE) of an organic light-emitting device (OLED), rather than just the chemical yield [13].

Critical Innovation: The research team used a "from-flask-to-device" approach, applying the crude reaction mixture directly to OLED fabrication. This eliminated energy-intensive purification steps, aligning with green chemistry principles, but added layers of complexity where interaction effects were likely [13].

DoE Protocol:

  • Factor Selection: Five factors known to influence the macrocyclization were selected:
    • Equivalent of Ni(cod)â‚‚ (M)
    • Dropwise addition time of reactant (T)
    • Final concentration of reactant (C)
    • % content of bromochlorotoluene in reactant (R)
    • % content of DMF in solvent (S) [13]
  • Experimental Design: An L18 Taguchi orthogonal array was used to define 18 distinct experimental runs, efficiently covering the 5-factor, 3-level parameter space [13].
  • Data Analysis and Machine Learning: The EQE data from the 18 experiments were used to train a Support Vector Regression (SVR) model. This model generated a predictive heatmap of EQE performance across the entire five-dimensional parameter space [13].
  • Validation: The model predicted an optimal condition (M=2, T=9, C=64, R=5, S=33) with a predicted EQE of 11.3%. A validation experiment at these conditions yielded a comparable EQE of 9.6%, confirming the model's accuracy [13].

The Decisive Outcome: Surpassing the Purified Standard

The device fabricated from the DoE-optimized crude mixture achieved an EQE of 9.6%. When the same device was fabricated using meticulously purified single compounds ([5]CMP or [6]CMP), the performance was drastically inferior (0.9% and 0.8% EQE, respectively) [13].

This result is a powerful demonstration of an interaction effect that OFAT could never have discovered. The optimal material was not a single, pure compound, but a specific mixture of congeners (n=5 to n=15) that acted synergistically to create an amorphous host material ideal for the solution-based spin-coating process. An OFAT approach, focused on isolating and testing single factors, would have led researchers to dismiss the crude mixture and settle on the vastly inferior pure compounds [13].

Comparative Analysis: OFAT vs. DoE

The table below provides a structured comparison of the two methodologies, highlighting the critical role of detecting interactions.

Table 1: A Systematic Comparison of OFAT and DoE Approaches

Feature One-Factor-at-a-Time (OFAT) Design of Experiments (DoE)
Core Principle Vary one factor while holding all others constant [2]. Vary multiple factors simultaneously according to a structured design [80].
Interaction Effects Cannot be detected or quantified. Assumes factors are independent [2] [80]. Can be detected, quantified, and modeled. A primary advantage of the method [80] [10].
Efficiency Inefficient; requires a large number of runs, especially as factors increase [2] [6]. Highly efficient; maximum information from a minimal number of experiments [81] [31].
Optimal Solution High risk of finding a local, sub-optimal solution [9]. High probability of finding the global, true optimum [81].
Exploration of Space Explores a single, narrow path through the experimental space, leaving "blank spots" [81] [6]. Systematically covers the entire experimental space, leaving no major areas unexplored [10].
Statistical Rigor Low; no inherent estimation of experimental error or statistical significance [2]. High; built-in principles of randomization, replication, and blocking ensure robust results [2].

Visualizing the Failure of OFAT

The following diagram illustrates a classic scenario where two factors (Temperature and Equivalents of Reagent) interact. OFAT's sequential path leads it to a sub-optimal solution, while DoE's comprehensive design directly identifies the region of optimal performance.

OFAT_Start OFAT Start: T=40, Eq=2 OFAT_1 Vary Eq at T=40 'Optimum' at Eq=2 OFAT_Start->OFAT_1 OFAT_2 Vary T at Eq=2 'Optimum' at T=55 OFAT_1->OFAT_2 OFAT_Miss Misses True Optimum: T=105, Eq=1.25 OFAT_2->OFAT_Miss DOE_Start DoE Design: Tests all corners and center point DOE_Model Builds Statistical Model (Incl. T*Eq Interaction) DOE_Start->DOE_Model DOE_Found Identifies True Optimum: T=105, Eq=1.25 DOE_Model->DOE_Found

Implementing DoE in Synthetic Workflows

For researchers seeking to adopt DoE, the following toolkit and workflow provide a practical starting point.

The Scientist's Toolkit: Essential Components for a DoE Study

Table 2: Key Reagents and Solutions for a DoE-driven Optimization

Item Function in the Workflow Example/Note
Taguchi Orthogonal Arrays Pre-defined statistical matrices for designing efficient experiments with multiple factors and levels [13]. Used in the case study to manage 5 factors at 3 levels in only 18 runs [13].
Definitive Screening Designs Specialized designs for screening a large number of factors with a minimal number of runs to identify the most influential ones. Ideal for initial phases of optimization with many potential variables [81].
Response Surface Methodologies (RSM) Designs (e.g., Central Composite, Box-Behnken) used for final optimization, modeling curvature and locating exact optimum conditions [2] [10]. Captures non-linear (quadratic) effects [10].
Machine Learning Algorithms Software tools (e.g., SVR, MLP) that use DoE data to build predictive models and visualize complex response surfaces [13]. SVR was the most accurate predictor in the case study [13].
Solvent Maps (PCA-Based) Tools for incorporating categorical variables like solvent into a DoE by representing solvent space with principle components [9]. Allows for systematic solvent optimization beyond trial-and-error [9].
Cholesteryl Arachidonate-d8Cholesteryl Arachidonate-d8, MF:C47H76O2, MW:681.2 g/molChemical Reagent
4-Isopropylphenyl Diphenyl Phosphate-d104-Isopropylphenyl Diphenyl Phosphate-d10, MF:C21H21O4P, MW:378.4 g/molChemical Reagent

A Practical Workflow for Reaction Optimization

  • Define the Objective: Identify the key responses (e.g., yield, selectivity, cost, device performance) and whether to maximize, minimize, or target a specific value [10].
  • Select Factors and Ranges: Choose the variables to study (e.g., temperature, concentration, catalyst) and set feasible high and low levels based on chemical knowledge [10].
  • Choose an Experimental Design: Start with a screening design for many factors, then move to a full factorial or response surface design for detailed optimization of critical factors [31] [10].
  • Execute and Analyze: Run the experiments, ideally in a randomized order. Use statistical software to analyze the data, identify significant main effects and interaction effects, and build a model [81] [10].
  • Validate the Model: Perform confirmation experiments at the predicted optimal conditions to verify the model's accuracy and the robustness of the solution [13] [10].

The evidence is clear: the One-Factor-at-a-Time approach is a fundamentally limited methodology for optimizing complex synthetic processes. Its inability to capture interaction effects between variables renders it inefficient and, more critically, prone to misleading conclusions and sub-optimal outcomes. As demonstrated in the OLED case study, these missed interactions can be the difference between a high-performing system and a failed one.

Design of Experiments provides the decisive statistical framework required for modern chemical research. By systematically exploring the experimental space and quantitatively modeling interactions, DoE empowers researchers to uncover synergistic effects, achieve true optimal performance, and accelerate the development of new synthetic methodologies and functional materials. For the drug development professional and research scientist, transitioning from OFAT to DoE is not merely a technical upgrade—it is a necessary paradigm shift to foster robust, efficient, and innovative science.

In the highly regulated and complex field of pharmaceutical development, achieving robust, efficient, and predictable processes is paramount. The traditional approach to process optimization, known as One Factor at a Time (OFAT), has been widely used but possesses fundamental limitations for understanding complex biological and chemical systems [6]. OFAT varies a single independent factor while keeping all others constant, which fails to detect interactions between factors and often misses the true optimal conditions for a process [82] [83].

In contrast, Design of Experiments (DoE) represents a systematic, statistical framework for process development that investigates multiple factors simultaneously to build mathematical models correlating input variables with output responses [82] [84]. When implemented within a Quality by Design (QbD) framework, DoE enables pharmaceutical scientists to design quality into products from the outset by establishing a design space—the multidimensional combination of input variables and process parameters demonstrated to provide assurance of quality [82] [83]. This whitepaper examines the real-world validation of DoE methodology in pharmaceutical process development, providing technical guidance for researchers and scientists seeking to implement this powerful approach.

DoE Versus OFAT: Fundamental Paradigms

Limitations of the OFAT Approach

The OFAT methodology, while straightforward and widely taught, suffers from several critical limitations in complex pharmaceutical environments:

  • Limited coverage of experimental space: OFAT examines only a small fraction of possible factor combinations, potentially missing optimal regions [6]
  • Failure to identify interactions: The approach cannot detect factor interactions, which are particularly important in biological systems where factors often influence each other [84] [83]
  • Inefficient resource utilization: OFAT typically requires more experimental runs to obtain less information compared to structured DoE approaches [6]
  • Risk of false optima: OFAT often identifies local optima while missing the global optimum, especially in systems with significant factor interactions [84] [85]

Advantages of the DoE Methodology

DoE addresses these limitations through a structured framework that offers significant advantages:

  • Systematic exploration: DoE provides thorough coverage of the experimental space with carefully selected factor combinations [6]
  • Interaction quantification: The methodology specifically models and quantifies interactions between factors, providing deeper process understanding [84]
  • Resource efficiency: DoE extracts maximum information from a minimal number of experimental runs, reducing time and material costs [86] [85]
  • Statistical robustness: Results are supported by statistical significance testing, providing confidence in conclusions [83]

Table 1: Fundamental Differences Between OFAT and DoE Approaches

Characteristic OFAT Approach DoE Approach
Factor Variation Sequential Simultaneous
Interaction Detection Not possible Explicitly modeled
Experimental Efficiency Low High
Statistical Foundation Limited Robust
Space Coverage Limited Comprehensive
Optima Identification Risk of false/local optima Global optima likely

DoE Implementation Framework

The Quality by Design (QbD) Paradigm

DoE finds its natural implementation within the QbD framework, which ICH Q8(R2) defines as "a systematic approach to development that begins with predefined objectives and emphasizes product and process understanding based on sound science and quality risk management" [82] [87]. The key components of QbD include:

  • Quality Target Product Profile (QTPP): A prospective summary of the quality characteristics of the drug product
  • Critical Quality Attributes (CQAs): Physical, chemical, biological, or microbiological properties or characteristics that should be within an appropriate limit, range, or distribution to ensure the desired product quality [87]
  • Critical Process Parameters (CPPs): Parameters whose variability impacts CQAs and therefore should be monitored or controlled to ensure the process produces the desired quality [87]
  • Critical Material Attributes (CMAs): Physical, chemical, biological, or microbiological properties or characteristics of input materials that should be within an appropriate limit, range, or distribution to ensure the desired product quality [82]
  • Design Space: The multidimensional combination and interaction of input variables and process parameters demonstrated to provide assurance of quality [82] [83]
  • Control Strategy: A planned set of controls derived from current product and process understanding that ensures process performance and product quality [87]

Structured DoE Workflow

A systematic approach to implementing DoE ensures comprehensive process understanding and robust results:

workflow Define Objective Define Objective Select Factors & Ranges Select Factors & Ranges Define Objective->Select Factors & Ranges Choose Experimental Design Choose Experimental Design Select Factors & Ranges->Choose Experimental Design Execute Randomized Runs Execute Randomized Runs Choose Experimental Design->Execute Randomized Runs Analyze Results & Build Model Analyze Results & Build Model Execute Randomized Runs->Analyze Results & Build Model Establish Design Space Establish Design Space Analyze Results & Build Model->Establish Design Space Verify & Validate Verify & Validate Establish Design Space->Verify & Validate Prior Knowledge Prior Knowledge Prior Knowledge->Select Factors & Ranges Risk Assessment Risk Assessment Risk Assessment->Select Factors & Ranges ATP/QTPP ATP/QTPP ATP/QTPP->Define Objective

Define Objective and Experimental Domain

Clear definition of study objectives is foundational to successful DoE implementation. Objectives may include factor screening, optimization, robustness testing, or design space characterization. Based on prior knowledge and risk assessment, researchers define the experimental domain by selecting factors and their appropriate ranges [83].

Select Appropriate Experimental Design

The choice of experimental design depends on the study objectives and number of factors:

  • Screening designs (e.g., Plackett-Burman, fractional factorials): Identify the most influential factors from a large set with minimal experimental runs [83] [85]
  • Response surface designs (e.g., Central Composite, Box-Behnken): Characterize curvature and locate optima in the experimental space [85]
  • Mixture designs: Specialized for formulating problems where components must sum to 100% [82]
  • Optimal designs: Computer-generated for complex constraints or unusual experimental regions
Execute Randomized Runs and Analyze Results

Experimental runs should be executed in randomized order to minimize confounding from uncontrolled variables. The resulting data is analyzed using statistical methods including Analysis of Variance (ANOVA), regression analysis, and graphical diagnostics to develop mathematical models relating factors to responses [83].

Real-World Case Studies

Pharmaceutical Pellet Manufacturing Process

A research scientist screened input factors for their effects on pellet yield in an extrusion-spheronization process, a well-known technology for developing multi-particulate dosage forms [83]. The study investigated five factors at two levels each using a fractional factorial design (2⁵⁻²III) with eight runs plus replication.

Table 2: Factors and Levels for Extrusion-Spheronization DoE

Input Factor Unit Lower Limit Upper Limit
Binder (B) % 1.0 1.5
Granulation Water (GW) % 30 40
Granulation Time (GT) min 3 5
Spheronization Speed (SS) RPM 500 900
Spheronization Time (ST) min 4 8

Table 3: Experimental Design and Response Data

Standard Run Order Binder (%) Granulation Water (%) Granulation Time (min) Spheronization Speed (RPM) Spheronization Time (min) Yield (%)
7 1.0 40 5 500 4 79.2
4 1.5 40 3 900 4 78.4
5 1.0 30 5 900 4 63.4
2 1.5 30 3 500 4 81.3
3 1.0 40 3 500 8 72.3
1 1.0 30 3 900 8 52.4
8 1.5 40 5 900 8 72.6
6 1.5 30 5 500 8 74.8

Statistical analysis revealed that all input variables except granulation time had significant effects on yield percentage. The percentage contribution of each factor to the total variation was: Binder (30.68%), Granulation Water (18.14%), Spheronization Speed (32.24%), and Spheronization Time (17.66%) [83]. This screening study efficiently identified critical factors for further optimization with minimal experimental runs.

Advanced Application: DoE with Machine Learning for OLED Development

In a cutting-edge application from 2025, researchers combined DoE with machine learning to optimize reaction conditions for organic light-emitting device (OLED) performance, demonstrating the methodology's applicability to complex, multi-step processes [13].

The study investigated five factors at three levels each using a Taguchi L18 orthogonal array design:

  • Equivalent of Ni(cod)â‚‚ (M)
  • Dropwise addition time of reactant (T)
  • Final concentration of reactant (C)
  • % content of bromochlorotoluene in reactant (R)
  • % content of DMF in solvent (S)

After conducting 18 reactions under the designed conditions, the crude products were directly used to fabricate OLED devices without purification. The external quantum efficiency (EQE) of each device was measured in quadruplicate. Researchers then applied machine learning methods—support vector regression (SVR), partial least squares regression (PLSR), and multilayer perceptron (MLP)—to model the relationship between reaction conditions and device performance [13].

The SVR model demonstrated the best predictive capability (mean square error = 0.0368) and successfully identified optimal reaction conditions that yielded a device with EQE = 9.6%, surpassing the performance of devices using purified materials (EQE = 0.9%) [13]. This approach eliminated energy-consuming purification steps while enhancing final device performance.

The Scientist's Toolkit: Essential Research Reagent Solutions

Table 4: Key Research Reagents and Materials for DoE Implementation

Reagent/Material Function in Experimental System Application Context
Ni(cod)â‚‚ Catalyst Mediates Yamamoto coupling macrocyclization OLED material synthesis [13]
DMF Solvent Affords reaction kinetics at disproportionation step Controlling product distribution in macrocyclization [13]
Bromochlorotoluene Reactant Varies oxidative addition kinetics Tweaking product distribution in macrocyclization [13]
Pharmaceutical Binders Promotes particle cohesion Pellet formation in extrusion-spheronization [83]
Ir Emitter Dopant Provides electroluminescent centers OLED device fabrication [13]
TPBi (1,3,5-tris(1-phenyl-1H-benzimidazol-2-yl)benzene) Electron transport material OLED electron transport layer [13]
(Z)-Tetrachlorvinphos-d6(Z)-Tetrachlorvinphos-d6, MF:C10H9Cl4O4P, MW:372.0 g/molChemical Reagent
rac 1-Palmitoyl-2-chloropropanediol-d5rac 1-Palmitoyl-2-chloropropanediol-d5, MF:C19H37ClO3, MW:354.0 g/molChemical Reagent

Implementation Challenges and Solutions

Despite its demonstrated advantages, DoE adoption in pharmaceutical and biotech industries faces several challenges:

  • Resource perception: DoE is sometimes perceived as requiring more experiments, though it actually provides more information per experiment [88]
  • Mindset and tradition: Experienced researchers may be accustomed to OFAT approaches and traditional development paths [88]
  • Training gap: Understanding of how to apply DoE effectively varies among researchers and managers [88]
  • Management understanding: Insufficient appreciation of DoE's power and overall efficiency, particularly when applied early in development [88]

Successful implementation strategies include:

  • Starting with screening designs to demonstrate value with manageable resource investment
  • Integrating DoE training with practical, project-based application
  • Building management awareness of DoE's long-term efficiency benefits
  • Leveraging software tools to simplify design generation and data analysis

Design of Experiments represents a fundamentally superior approach to pharmaceutical process development compared to traditional OFAT methodology. Through systematic, simultaneous variation of multiple factors, DoE enables efficient identification of critical process parameters, quantification of their interactions, and establishment of robust design spaces. Real-world case studies across diverse applications—from pharmaceutical pellet manufacturing to advanced OLED materials development—demonstrate DoE's ability to enhance process understanding, improve product quality, reduce development costs, and accelerate timelines.

When implemented within a QbD framework, DoE provides the scientific foundation for regulatory flexibility through demonstrated process understanding. As pharmaceutical development grows increasingly complex, embracing DoE methodology becomes essential for researchers and drug development professionals seeking to optimize processes efficiently and ensure the highest quality standards in pharmaceutical products.

In the field of organic synthesis, the pursuit of optimal reaction conditions is a fundamental and time-consuming endeavor. For decades, the One-Factor-at-a-Time (OFAT) approach has been a cornerstone of laboratory optimization, relying on systematic variation of individual parameters while holding others constant [3] [2]. However, this traditional methodology is increasingly being supplanted by the statistically rigorous framework of Design of Experiments (DoE), which enables the simultaneous investigation of multiple factors and their interactions [21] [9]. This paradigm shift is particularly evident in pharmaceutical development and academic research, where efficiency, sustainability, and comprehensive process understanding are paramount [9] [49].

The critical limitation of OFAT lies in its inherent inability to detect interaction effects between factors, potentially leading researchers to suboptimal conditions and incomplete mechanistic understanding [2] [9]. In contrast, DoE employs structured experimental designs to efficiently explore the multi-dimensional parameter space, quantifying both main effects and factor interactions while providing statistical robustness through principles of randomization, replication, and blocking [2] [21]. This comparative analysis examines these methodologies across key performance metrics, providing synthetic chemists with a framework for selecting appropriate optimization strategies in research and development.

Theoretical Foundations and Methodological Principles

One-Factor-at-a-Time (OFAT) Optimization

The OFAT methodology, also known as the classical or hold-one-factor-at-a-time approach, involves systematically examining the effect of individual factors on a response while maintaining all other factors at constant levels [2]. The procedure typically follows these steps: (1) selection of baseline conditions for all factors; (2) variation of one factor across different levels while keeping others static; (3) observation of the response; (4) returning the varied factor to its baseline before investigating the next factor [2]. This cycle continues until all factors of interest have been tested independently, with the optimal conditions being determined by combining the individually optimized parameters [21].

Despite its historical prevalence and intuitive appeal, OFAT operates on the flawed assumption that factors do not interact with each other, an assumption rarely valid in complex chemical systems [2] [9]. The methodology is primarily focused on understanding individual factor effects rather than providing a systematic approach for global optimization [2]. Furthermore, OFAT requires a large number of experimental runs, especially with multiple factors, leading to inefficient resource utilization and increased risk of experimental error due to the extensive manual operations involved [2] [21].

Design of Experiments (DoE) Optimization

DoE represents a paradigm shift from OFAT, employing a systematic, statistically-based approach to investigate the relationship between multiple input factors and output responses simultaneously [2] [9]. The methodology is built upon three fundamental principles: randomization (conducting experimental runs in random order to minimize the impact of lurking variables), replication (repeating experimental runs to estimate experimental error), and blocking (grouping runs to account for known sources of variability) [2].

The typical DoE workflow encompasses several key stages [49]:

  • Objective Definition: Identifying process issues, typically focusing on optimization, robustness testing, or factor screening.
  • Factor and Range Specification: Selecting factors for inclusion and establishing practical high and low settings based on existing process knowledge.
  • Response Definition: Establishing measurable outcomes (e.g., yield, purity, selectivity) with accuracy ensured through replicated center points.
  • Experimental Design Selection: Choosing an appropriate design (e.g., factorial, response surface, screening) based on objectives and resources.
  • Experiment Execution: Performing reactions according to the design, often in randomized run order.
  • Data Analysis and Modeling: Inputting results for statistical analysis, selecting mathematical models based on key metrics (p-values, R-squared).
  • Validation: Experimentally confirming ideal conditions suggested by the DoE analysis.

DoE offers several distinct advantages over OFAT, including the ability to study factor interactions, improved experimental efficiency, estimation of experimental error, optimization capabilities through response surface methodology, and enhanced robustness and reliability of results [2].

Comparative Performance Analysis

Table 1: Comprehensive comparison of OFAT and DoE across key performance metrics

Performance Metric OFAT (One-Factor-at-a-Time) DoE (Design of Experiments)
Experimental Efficiency Inefficient; requires many runs ( [2] [21]). Example: 3 levels for 5 factors = 3⁵ = 243 experiments ( [21]). Highly efficient; explores multiple factors simultaneously. Example: 5 factors in 19 experiments using Resolution IV design ( [9]).
Interaction Detection Cannot detect interactions between factors ( [2] [9]). Assumes factors are independent. Specifically designed to identify and quantify interactions ( [2] [9]).
Optimization Capability Limited; finds improved conditions, not necessarily global optimum ( [2] [21]). Comprehensive; identifies true optimal conditions, including trade-offs in multi-objective optimization ( [3]).
Statistical Robustness Low; no inherent estimation of experimental error or significance ( [2]). High; incorporates replication, randomization, and blocking for reliable results ( [2]).
Resource Consumption High resource use (time, materials) per unit of information gained ( [2] [21]). Optimal resource utilization; maximum information from minimal experiments ( [2] [49]).
Basis of Design Chemist's intuition and sequential observation ( [3] [21]). Statistical principles and structured experimental designs ( [2] [9]).
Application Complexity Simple to design but tedious to execute for multiple factors ( [3]). Requires statistical understanding but software tools lower barrier ( [3] [9]).
Risk of Misleading Results High; can miss optimal conditions due to factor interactions ( [2] [9]). Low; maps comprehensive response surfaces to avoid false optima ( [9]).
Process Understanding Limited to main effects only ( [21]). Comprehensive; reveals system behavior through interactions and response surfaces ( [21] [89]).

Case Study: DoE and Machine Learning in OLED Material Synthesis

A recent groundbreaking application of advanced optimization demonstrated the power of combining DoE with machine learning (ML) in multistep device fabrication processes [13]. Researchers developed a "from-flask-to-device" methodology for optimizing a macrocyclization reaction yielding a mixture of methylated [n]cyclo-meta-phenylenes, where the crude reaction mixture was directly used to fabricate Ir-doped organic light-emitting devices (OLEDs) via spin-coating [13].

Experimental Protocol

The study employed an integrated DoE+ML approach with the following detailed methodology [13]:

  • Factor Selection: Five factors previously identified as influential in Yamamoto macrocyclization were selected: equivalent of Ni(cod)â‚‚ (M), dropwise addition time of dihalotoluene 1 (T), final concentration of 1 (C), percentage content of bromochlorotoluene in 1 (R), and percentage content of DMF in solvent (S).

  • Experimental Design: Three levels were examined for each factor, requiring an L18 (2¹ × 3⁷) orthogonal array from Taguchi's system to define the DoE parameter space.

  • Reaction Execution: Eighteen Yamamoto macrocyclization reactions were performed under the designed conditions. Crude raw materials were obtained after aqueous workup and passage through a short-path silica gel column to remove metal and polar residues.

  • Device Fabrication and Evaluation: Double-layer OLEDs were fabricated from each material by spin-coating a solution of the crude mixture mixed with an Ir emitter (14 wt% in layer) as a 20 nm emission layer, followed by sublimation of TPBi as a 60 nm electron transport layer. Device performance was evaluated by external quantum efficiency (EQE) in quadruplicate.

  • Machine Learning Integration: Three ML methods—support vector regression (SVR), partial least squares regression (PLSR), and multilayer perceptron (MLP)—were investigated to generate EQE heatmaps. The SVR model demonstrated superior performance with the lowest mean square error (0.0368) in leave-one-out cross-validation.

  • Validation: The optimized SVR model predicted an optimal EQE of 11.3% at specific factor settings (M=2, T=9, C=64, R=5, S=33). Experimental validation achieved a comparable EQE of 9.6±0.1%, confirming the model's predictive accuracy [13].

Comparative Outcome

This integrated approach yielded significant advantages over traditional methods:

  • Performance Superiority: The OLED fabricated with the optimal raw mixture achieved an EQE of 9.6%, surpassing devices using purified materials (EQE = 0.9±0.1% for n=5 and 0.8±0.3% for n=6 congeners) [13].

  • Process Simplification: The methodology eliminated energy-consuming and waste-producing separation and purification steps, aligning with green chemistry principles [13].

  • Material Characterization: Analysis of the optimal raw material revealed a complex mixture of methylated [n]CMP congeners (n=5 to 15), suggesting the amorphous character of the mixture contributed to superior performance compared to crystalline pure materials [13].

OLED_Optimization DoE+ML Workflow for OLED Material Optimization Start Define Optimization Objective DoE DoE Design: 5 Factors, 3 Levels L18 Orthogonal Array Start->DoE Experiment Execute 18 Reactions Under DoE Conditions DoE->Experiment Device Fabricate OLED Devices from Crude Materials Experiment->Device Measure Measure Device Performance (EQE) Device->Measure ML Machine Learning (SVR Model Training) Measure->ML Predict Predict Optimal Reaction Conditions ML->Predict Validate Experimental Validation Predict->Validate End Optimal Conditions for OLED Performance Validate->End

Figure 1: DoE+ML workflow for OLED material optimization integrating experimental design with machine learning prediction.

Experimental Design and Protocol Guidelines

DoE Implementation Framework

Successful implementation of DoE in organic synthesis requires a structured approach:

  • Pre-experimental Planning: Clearly define optimization objectives and identify all potentially influential factors through preliminary screening experiments. Establish practical ranges for each factor based on chemical feasibility and safety considerations [49].

  • Design Selection: For initial screening when many factors are involved, fractional factorial or Plackett-Burman designs efficiently identify significant factors. For optimization studies with fewer factors, response surface methodologies (RSM) such as Central Composite Designs (CCD) or Box-Behnken designs provide detailed mapping of the response surface [12] [89].

  • Modeling and Analysis: Employ statistical software (JMP, MODDE, Design-Expert, or Python/R packages) to analyze results and build mathematical models relating factors to responses. Validate models through statistical indicators (R², adjusted R², prediction error sum of squares) and confirmatory experiments [90].

Response Surface Methodology

Response Surface Methodology (RSM) is a powerful optimization technique within DoE that builds mathematical models to describe the behavior of response variables as functions of input factors [89]. The methodology typically employs sequential experimentation:

  • Initial Factorial Design: A full or fractional factorial design establishes a linear model in the region of interest.
  • Path of Steepest Ascent: The model determines the direction of maximum improvement, guiding a series of sequential experiments toward the optimum region.
  • Refined Modeling: Once near the optimum, a second-order model (e.g., Central Composite Design) captures curvature and enables precise location of the optimum [89].

A representative RSM optimization for a bioreactor system demonstrated how moving along the path of steepest ascent increased profit from $407 to $669 per day, with further refinement achieving $688 profit before decline indicated overshooting the optimum [89].

The Scientist's Toolkit: Essential Research Reagents and Solutions

Table 2: Key research reagents and computational tools for modern reaction optimization

Reagent/Solution Function in Optimization Application Example
PdClâ‚‚(MeCN)â‚‚ Catalyst Homogeneous catalyst for oxidation reactions Wacker-type oxidation of 1-decene to n-decanal [49]
Ni(cod)â‚‚ Catalyst Mediator for Yamamoto coupling macrocyclization Synthesis of methylated [n]cyclo-meta-phenylenes for OLEDs [13]
Orthogonal Array Solvents Representative solvents covering chemical space DoE solvent optimization using principle component analysis [9]
Central Composite Design Response surface design for quadratic modeling Process optimization with center points and axial points [89] [91]
Box-Behnken Design Efficient spherical RSM design for 3-7 factors Phytochemical extraction optimization [91]
DoE Software (JMP, MODDE) Statistical design and analysis of experiments Generating experimental designs and modeling response surfaces [21] [90]
Machine Learning Algorithms Predictive modeling of complex reaction outcomes SVR, PLSR, and MLP for reaction condition prediction [13]
O-Desmethyl Mebeverine acid-d6O-Desmethyl Mebeverine acid-d6, MF:C15H23NO3, MW:271.38 g/molChemical Reagent
Betamethasone 17-Propionate-d5Betamethasone 17-Propionate-d5, MF:C25H33FO6, MW:453.6 g/molChemical Reagent

The comparative analysis unequivocally demonstrates the superior performance of DoE across virtually all key metrics in reaction optimization. While OFAT retains value for simple systems with minimal factor interactions or initial exploratory studies, its limitations in efficiency, optimization capability, and interaction detection render it inadequate for complex synthetic challenges in modern organic chemistry and drug development [2] [21] [9].

The integration of DoE with machine learning represents the cutting edge of reaction optimization, enabling correlation of reaction conditions with complex performance metrics even in multistep processes [13]. Furthermore, the alignment of DoE with Green Chemistry principles through reduced solvent and reagent consumption positions it as an essential methodology for sustainable chemical development [49] [91].

As the chemical sciences continue to emphasize efficiency, sustainability, and systematic understanding, the adoption of statistically-based optimization methodologies will be imperative for researchers seeking to advance synthetic methodology and process development in academic and industrial settings.

Conclusion

The transition from OFAT to DoE represents a paradigm shift in how synthetic chemistry optimization is approached. While OFAT offers simplicity, it is a high-risk strategy that often fails to find true optima and misses critical interaction effects, leading to inefficient use of valuable resources. DoE, in contrast, provides a systematic, data-driven framework that not only identifies optimal conditions with fewer experiments but also builds a profound understanding of the reaction landscape. The integration of machine learning with DoE, as seen in cutting-edge research, further enhances its predictive power. For the biomedical and clinical research fields, adopting DoE promises accelerated drug development timelines, more robust and scalable synthetic processes, and a deeper mechanistic understanding of complex chemical transformations, ultimately contributing to the faster delivery of new therapeutics.

References